八大排序算法的代码实现和时空复杂度比较。
| 排序法 |
平均时间 |
最差情形 |
稳定度 |
额外空间 |
备注 |
| ⭐插入 |
|
|
稳定 |
|
大部分已排序时较好 |
| ⭐冒泡 |
|
|
稳定 |
|
小时较好 |
| ⭐选择 |
|
|
不稳定 |
|
小时较好 |
| ⭐快排 |
|
|
不稳定 |
|
大时较好 |
| ⭐堆 |
|
|
不稳定 |
|
大时较好 |
| ⭐归并 |
|
|
稳定 |
|
大时较好 |
| 基数 |
|
|
稳定 |
|
是真数(0-9),是基数(个十百) |
| 希尔 |
|
|
不稳定 |
|
是所选分组 |
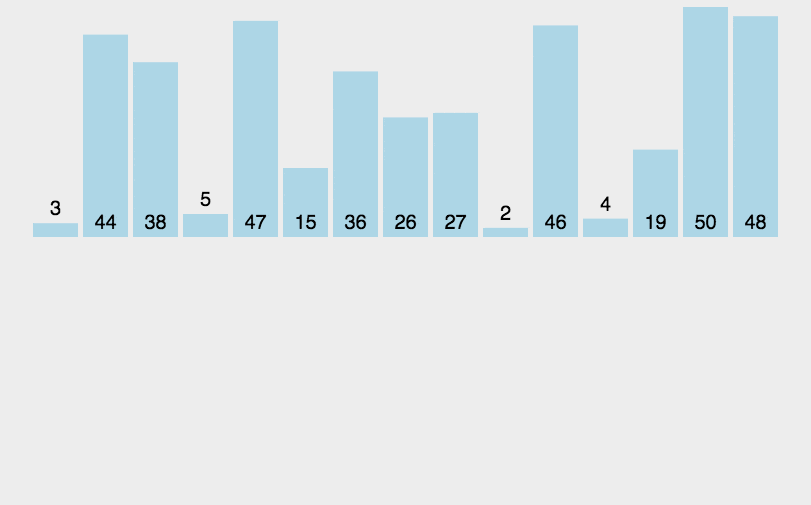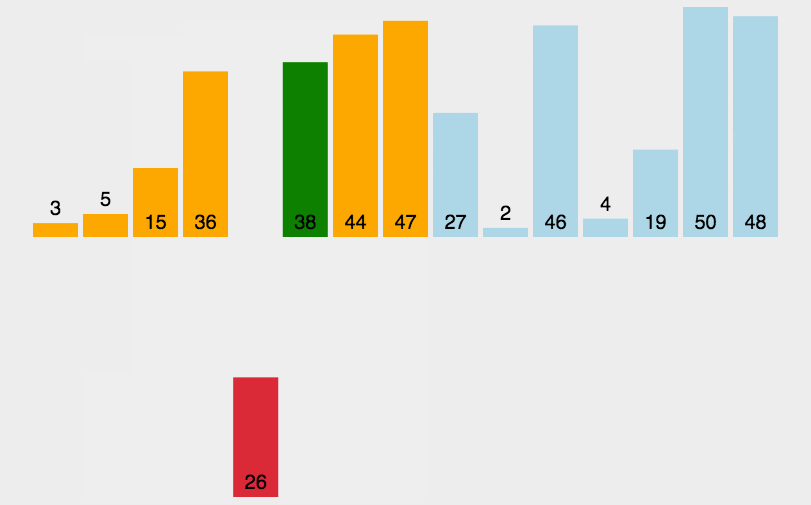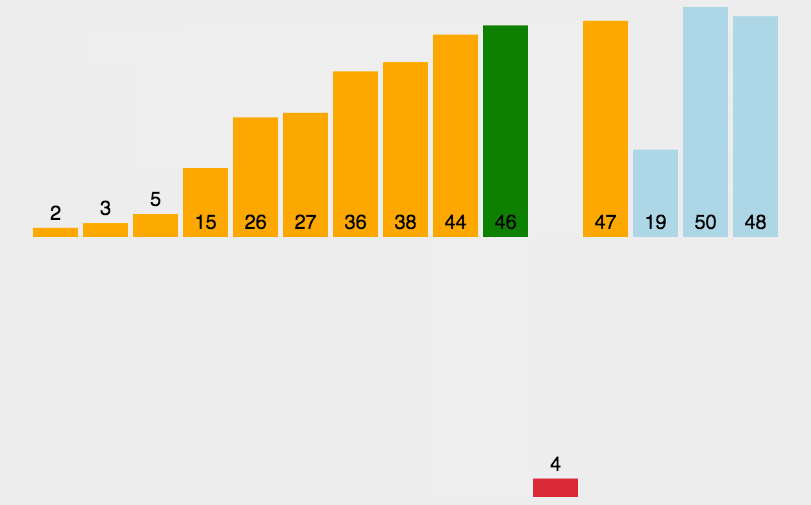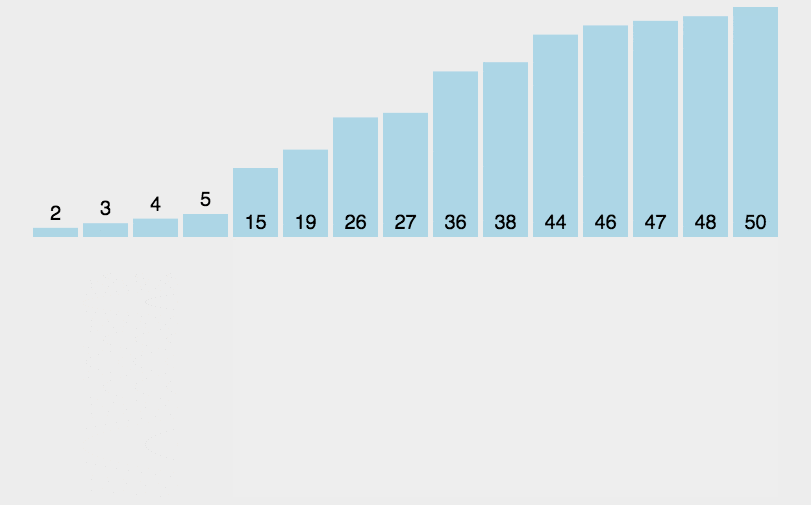
插入
将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
/**
* 从第二个元素开始,插入到前面已经有序的序列中,即找到序列中第一个小于等于当前元素的,将这以后的元素都
* 向后移一位,然后将当前元素插入到这个位置中
*
* @param arr
*/
public void insertionSort(int[] arr) {
/*
0 1 2 ...i-1 i i+1 ... n-1
对于下标 i,[0, i-1]此时已经有序,将i插入到[0, i-1]中
具体操作是找到i应该插入的下标idx,将[idx, i-1]的元素后移,
将i元素放到idx+1(最后一个比新元素更大的位置是下标idx,但是循环中idx最后一次还是会往左减一
因此要放到idx+1处
*/
int n = arr.length;
for (int i = 0; i < n; i++) {
int cur_val = arr[i];
int idx = i - 1;
while (idx >= 0 && arr[idx] > cur_val) {
arr[idx + 1] = arr[idx];
idx--;
}
arr[idx + 1] = cur_val;
}
}
|
冒泡
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
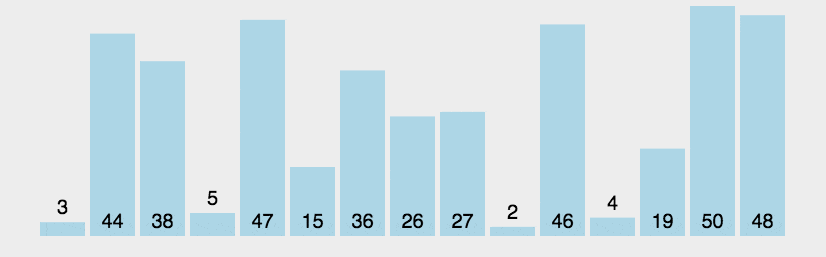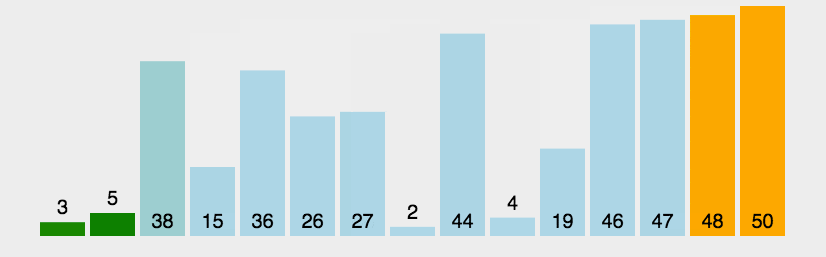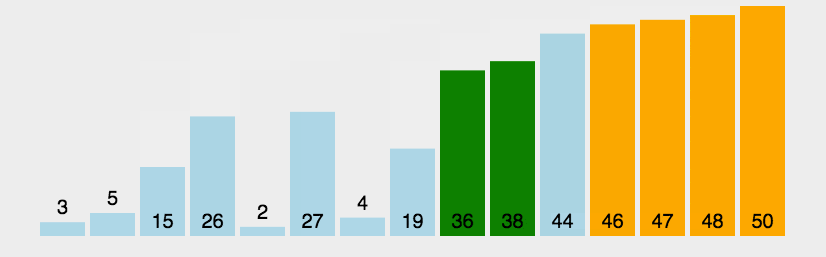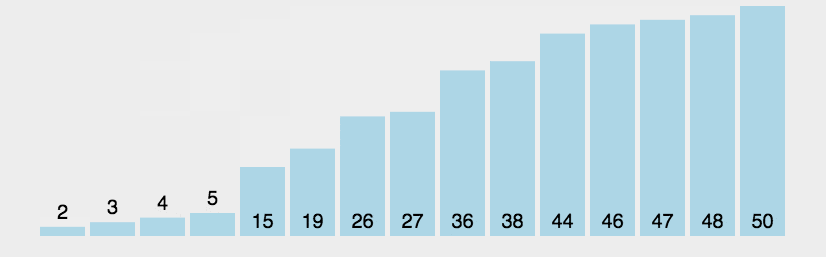
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
/**
* 一共n个元素,每轮将一个元素冒泡到最后的位置
* 对于第i轮,需要冒泡一个元素到第n-1-i的位置,因此需要从[0,1],[1,2], ..., [n-1-i-1,n-1-i]每次将较大的元素往后放
* 为了优化已经有序的情况,可以设置flag记录是否已经有序
* 如果当轮存在交换则将flag置为false表示未有序,如果flag为true说明前面的元素已经有序了
*
* @param arr
*/
public void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) { // 每轮将一个最大的元素沉到最后
boolean flag = true; // 当前轮是否有序
for (int j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
flag = false; // 未有序
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
if (flag) break; // 有序
}
}
|
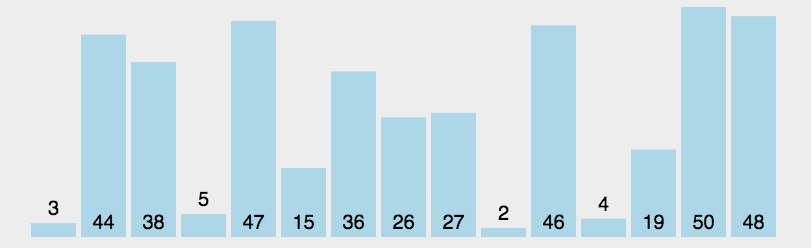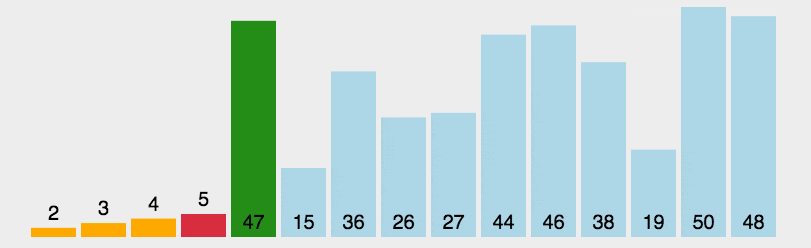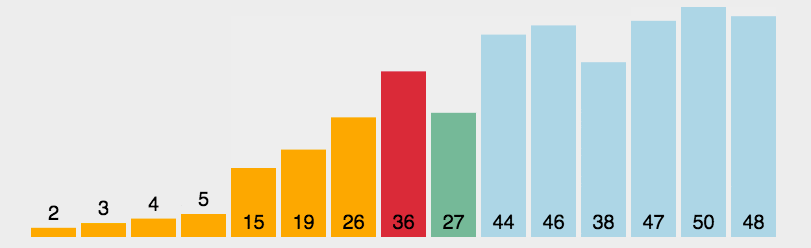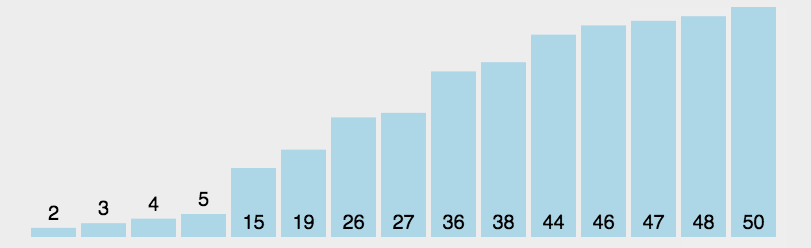
选择
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
/**
* 对于每个位置我们插入其应当有的元素,即对于第0位置的元素,我们找到最小的然后和这个位置的元素进行交换
*
* @param arr
*/
public void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
int min_index = i;
for (int j = i; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;
}
}
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
|
快排
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
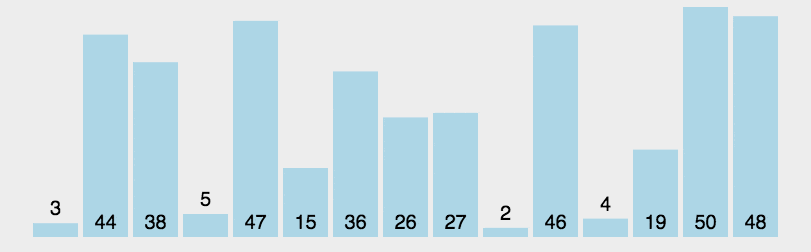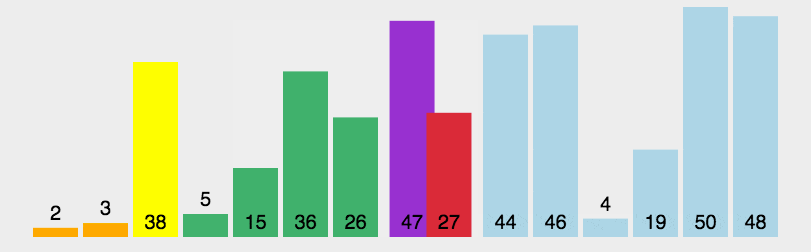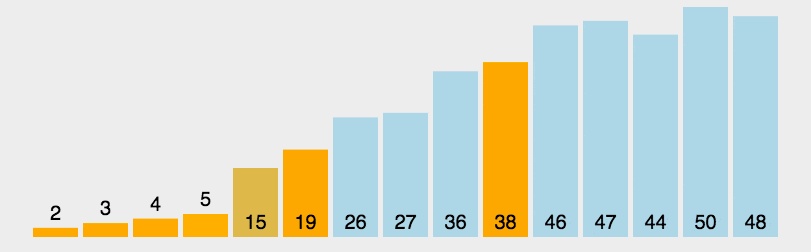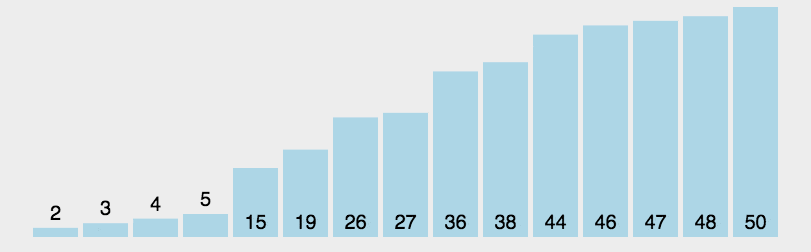
递归版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public void quickSort(int[] arr) {
quickSortRange(arr, 0, arr.length - 1);
}
public void quickSortRange(int[] arr, int left, int right) {
if (left < right) {
int mid = partition(arr, left, right);
quickSortRange(arr, left, mid - 1);
quickSortRange(arr, mid + 1, right);
}
}
private int partition(int[] arr, int left, int right) {
int pivot = arr[left];
while (left < right) {
while (left < right && arr[right] >= pivot) {
right--;
}
arr[left] = arr[right];
while (left < right && arr[left] <= pivot) {
left++;
}
arr[right] = arr[left];
}
arr[left] = pivot;
return left;
}
|
非递归版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
public void quickSort(int[] nums) {
stackQuickSort(nums, 0, nums.length - 1);
}
public void stackQuickSort(int[] nums, int left, int right) {
Deque<Integer> stack = new LinkedList<>();
if (left < right) {
stack.push(right);
stack.push(left);
}
while (!stack.isEmpty()) {
int l = stack.pop();
int r = stack.pop();
int mid = partition(nums, l, r);
// 得到mid后划分为 [l, mid - 1] mid [mid + 1, r]
if (l < mid - 1) {
stack.push(mid - 1);
stack.push(l);
}
if (r > mid + 1) {
stack.push(r);
stack.push(mid + 1);
}
}
}
private int partition(int[] nums, int left, int right) {
int pivot = nums[left];
while (left < right) {
while (left < right && nums[right] >= pivot) {
right--;
}
nums[left] = nums[right];
while (left < right && nums[left] <= pivot) {
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
}
|
堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
public void heapSort(int[] arr) {
int len = arr.length;
buildMaxHeap(arr, len);
for (int i = len - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
}
private void buildMaxHeap(int[] arr, int len) {
for (int i = len / 2 - 1; i >= 0; i--) {
heapify(arr, i, len);
}
}
private void heapify(int[] arr, int i, int len) {
while (true) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest == i) break;
swap(arr, i, largest);
i = largest;
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
|
归并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
/**
* 归并排序
* @param arr
* @return
*/
public int[] mergeSort(int[] arr) {
if (arr == null || arr.length <= 1) return arr;
int n = arr.length;
int mid = n / 2;
int[] left = Arrays.copyOfRange(arr, 0, mid);
int[] right = Arrays.copyOfRange(arr, mid, n);
return merge(mergeSort(left), mergeSort(right));
}
private int[] merge(int[] a, int[] b) {
int[] res = new int[a.length + b.length];
int i = 0, j = 0, ind = 0;
while (i < a.length && j < b.length) {
res[ind++] = (a[i] < b[j]) ? a[i++] : b[j++];
}
while (i < a.length) {
res[ind++] = a[i++];
}
while (j < b.length) {
res[ind++] = b[j++];
}
return res;
}
|
希尔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
/**
* 希尔排序,减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
* @param arr
*/
public void shellSort(int[] arr) {
int n = arr.length;
for (int gap = n / 2; gap > 0; gap /= 2) {
// {i, i+gap, i+2gap, ...}
for (int i = 0; i < n; i++) {
int cur_val = arr[i];
int idx = i - gap;
while (idx >= 0 && arr[idx] > cur_val) {
arr[idx + gap] = arr[idx];
idx -= gap;
}
arr[idx + gap] = cur_val;
}
}
}
|