LeetCode 按照分类刷完 HOT 100 以及相关题目,再加上剑指 Offer,应对实习和秋招应该可以。
HOT 100
回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// 主函数里面先对集合排序
/*
回溯:
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素) { // 横向处理
// 对于有重复元素的情况要加上以下判断
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
处理节点;
dfs(路径,选择列表); // 纵向递归
回溯,撤销处理结果
}
}
*/
|
组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
dfs(1, n, k);
return res;
}
private void dfs(int begin, int n, int k) {
if (path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// 如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
// 已经选择的元素个数:path.size();
// 还需要的元素个数为: k - path.size();
// n-i+1 >= k - path.size()
// i <= n+1-(k - path.size())
// 在集合n中至多要从该起始位置 : n + 1 - (k - path.size()),开始遍历
for (int i = begin; i <= n + 1 - (k - path.size()); i++) {
path.add(i);
dfs(i + 1, n, k);
path.remove(path.size() - 1);
}
}
}
|
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
List<String> res = new ArrayList<>();
String[] map = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
StringBuilder sb = new StringBuilder();
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) return res;
dfs(digits, 0);
return res;
}
private void dfs(String digits, int index) {
if (sb.length() == digits.length()) { // 递归出口
res.add(sb.toString());
return;
}
char[] choices = map[digits.charAt(index) - '2'].toCharArray(); // 处理当前层
for (char ch : now.toCharArray()) { // 选择本层集合中的元素ch
sb.append(ch); // 处理节点
dfs(digits, index + 1); // 递归
sb.deleteCharAt(sb.length() - 1); // 回溯,撤销上面处理的节点
}
}
}
|
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ,找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同,则两种组合是唯一的。
对于给定的输入,保证和为 target 的唯一组合数少于 150 个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
dfs(candidates, 0, target);
return res;
}
private void dfs(int[] candidates, int begin, int target) {
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
if (target < 0) return; // 纵向剪枝
for (int i = begin; i < candidates.length; i++) {
if (target - candidates[i] < 0) break; // beat 10% -> 96%,横向剪枝
path.add(candidates[i]);
dfs(candidates, i, target - candidates[i]); // 下一次i位置的元素还可以选
path.remove(path.size() - 1);
}
}
}
|
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
**注意:**解集不能包含重复的组合。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
boolean[] used = new boolean[candidates.length];
dfs(candidates, 0, target, used);
return res;
}
private void dfs(int[] candidates, int begin, int target, boolean[] used) {
if (target < 0) return;
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < candidates.length; i++) {
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
if (target - candidates[i] < 0) break; // beat 14% -> 98%
path.add(candidates[i]);
used[i] = true;
dfs(candidates, i + 1, target - candidates[i], used);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
|
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
dfs(k, n, 1);
return res;
}
private void dfs(int k, int n, int begin) {
if (k == 0 && n == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i <= 9; i++) {
path.add(i);
dfs(k - 1, n - i, i + 1);
path.remove(path.size() - 1);
}
}
}
|
排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
boolean[] used = new boolean[nums.length];
dfs(nums, used);
return res;
}
private void dfs(int[] nums, boolean[] used) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
if (used[i] == false) {
path.add(nums[i]);
used[i] = true;
dfs(nums, used);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
}
|
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
boolean[] used = new boolean[nums.length];
dfs(nums, used);
return res;
}
private void dfs(int[] nums, boolean[] used) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
// 在上一题的基础上加了这句判断
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
if (used[i] == false) {
path.add(nums[i]);
used[i] = true;
dfs(nums, used);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
}
|
分割
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
List<List<String>> res = new ArrayList<>();
List<String> path = new ArrayList<>();
public List<List<String>> partition(String s) {
dfs(s, 0);
return res;
}
private void dfs(String s, int begin) {
if (begin == s.length()) { // 分割到字符串最后结束
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < s.length(); i++) {
if (isReverse(s.substring(begin, i + 1))) {
path.add(s.substring(begin, i + 1));
dfs(s, i + 1);
path.remove(path.size() - 1);
}
}
}
private boolean isReverse(String s) {
int len = s.length();
int left = 0, right = len - 1;
while (left < right) {
if (s.charAt(left) != s.charAt(right)) return false;
left++;
right--;
}
return true;
}
}
|
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
- 例如:
"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "[email protected]" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
List<String> res = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if (s.length() > 12) return res;
dfs(s, 0, 0);
return res;
}
// 相较于上题,这道题限制了组合的次数,也就是规定只能割3次
private void dfs(String s, int begin, int pointCnt) {
if (pointCnt == 3) { // 分割了3次结束
if (isValid(s.substring(begin, s.length()))) {
res.add(s);
return;
}
}
for (int i = begin; i < s.length(); i++) {
if (isValid(s.substring(begin, i + 1))) {
s = s.substring(0, i + 1) + '.' + s.substring(i + 1);
pointCnt++;
dfs(s, i + 2, pointCnt);
pointCnt--;
s = s.substring(0, i + 1) + s.substring(i + 2);
}
}
}
// 判断是否合法
private boolean isValid(String s) {
if (s == null || s.length() == 0) return false;
if (s.length() > 1 && s.charAt(0) == '0') return false;
if (s.length() > 4) return false;
int val = 0;
for (char c : s.toCharArray()) {
if (!(c >= '0' && c <= '9')) return false;
val = val * 10 + (c - '0');
}
return val >= 0 && val <= 255;
}
}
|
子集
子集问题类似于组合问题,都是使用begin。排列问题使用used数组。
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
if (nums == null || nums.length == 0) return res;
dfs(nums, 0);
return res;
}
private void dfs(int[] nums, int begin) {
res.add(new ArrayList<>(path));
for (int i = begin; i < nums.length; i++) {
path.add(nums[i]);
dfs(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
|
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 在上一题基础上使用used数据处理去重
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
if (nums == null || nums.length == 0) return res;
boolean[] used = new boolean[nums.length];
Arrays.sort(nums);
dfs(nums, used, 0);
return res;
}
private void dfs(int[] nums, boolean[] used, int begin) {
res.add(new ArrayList<>(path));
for (int i = begin; i < nums.length; i++) {
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
path.add(nums[i]);
used[i] = true;
dfs(nums, used, i + 1);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
|
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
if (nums == null || nums.length == 0) return res;
dfs(nums, 0);
return res;
}
private void dfs(int[] nums, int begin) {
if (path.size() >= 2) {
res.add(new ArrayList<>(path));
// 注意这里不要加return,要取树上的节点
}
Set<Integer> set = new HashSet<>(); // 使用set对本层元素进行去重
for (int i = begin; i < nums.length; i++) {
if (set.contains(nums[i]) || (!path.isEmpty() && nums[i] < path.get(path.size() - 1))) continue;
set.add(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了,对于本层的其他分支,自然也就不用撤回这个选择
path.add(nums[i]);
dfs(nums, i + 1);
path.remove(path.size() - 1);
}
}
}
|
棋盘
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] board = new char[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i][j] = '.';
}
}
dfs(0, n, board);
return res;
}
private void dfs(int row, int n, char[][] board) {
if (row == n) {
res.add(new ArrayList<>(transfer(board)));
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, n, board)) {
board[row][col] = 'Q';
dfs(row + 1, n, board);
board[row][col] = '.';
}
}
}
private List<String> transfer(char[][] board) {
List<String> res = new ArrayList<>();
for (int i = 0; i < board.length; i++) {
res.add(String.valueOf(board[i]));
}
return res;
}
private boolean isValid(int row, int col, int n, char[][] board) {
// 竖线
for (int i = 0; i < row; i++) {
if (board[i][col] == 'Q') return false;
}
// 45°
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q') return false;
}
// 135°
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') return false;
}
return true;
}
}
|
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9 在每一行只能出现一次。
- 数字
1-9 在每一列只能出现一次。
- 数字
1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
数独部分空格内已填入了数字,空白格用 '.' 表示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public void solveSudoku(char[][] board) {
dfs(board);
}
private boolean dfs(char[][] board) {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
// 对于每一个空的地方尝试插入元素
if (board[i][j] != '.') continue;
for (char value = '1'; value <= '9'; value++) {
if (isValid(board, i, j, value)) {
board[i][j] = value;
if (dfs(board)) {
return true;
}
board[i][j] = '.';
}
}
return false;
}
}
return true;
}
// 判断是否可以插入元素value
private boolean isValid(char[][] board, int row, int col, char value) {
for (int j = 0; j < 9; j++) {
if (board[row][j] == value) return false;
}
for (int i = 0; i < 9; i++) {
if (board[i][col] == value) return false;
}
int beginRow = (row / 3) * 3, beginCol = (col / 3) * 3;
for (int i = beginRow; i < beginRow + 3; i++) {
for (int j = beginCol; j < beginCol + 3; j++) {
if (board[i][j] == value) {
return false;
}
}
}
return true;
}
}
|
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9 在每一行只能出现一次。
- 数字
1-9 在每一列只能出现一次。
- 数字
1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public boolean isValidSudoku(char[][] board) {
// 记录某行,某位数字是否已经被摆放
boolean[][] row = new boolean[9][9];
// 记录某列,某位数字是否已经被摆放
boolean[][] col = new boolean[9][9];
// 记录某 3x3 宫格内,某位数字是否已经被摆放
boolean[][] block = new boolean[9][9];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
int num = board[i][j] - '1';
int blockIndex = i / 3 * 3 + j / 3;
if (row[i][num] || col[j][num] || block[blockIndex][num]) {
return false;
} else {
row[i][num] = true;
col[j][num] = true;
block[blockIndex][num] = true;
}
}
}
}
return true;
}
}
|
岛屿问题
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public int numIslands(char[][] grid) {
int res = 0;
int m = grid.length, n = grid[0].length;
boolean[][] visited = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1' && !visited[i][j]) {
dfs(grid, visited, i, j);
res++;
}
}
}
return res;
}
private void dfs(char[][] grid, boolean[][] visited, int i, int j) {
if (!check(grid, i, j) || visited[i][j] || grid[i][j] == '0') return;
visited[i][j] = true;
dfs(grid, visited, i + 1, j);
dfs(grid, visited, i - 1, j);
dfs(grid, visited, i, j + 1);
dfs(grid, visited, i, j - 1);
}
private boolean check(char[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
return i >= 0 && i < m && j >= 0 && j < n;
}
}
|
不用额外的空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
// 不用额外的visited,每次遍历完1后将其置为2表示已访问
public int numIslands(char[][] grid) {
int row = grid.length, col = grid[0].length;
int res = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (grid[i][j] == '1') {
dfs(grid, i, j);
res++;
}
}
}
return res;
}
private void dfs(char[][] grid, int i, int j) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1') return;
grid[i][j] = '2';
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
|
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
/**
* 岛屿的周围就是,一个岛屿格子的边与地图边界或者海洋的部分相交的话,那么这条边就是岛屿的周长的一部分。
dfs即从i,j这个岛屿开始涂色,涂色的时候发现当前是边界或者是海洋,那么当前边就算入周长中,否则的话如果当前已经涂过色,直接return,否则继续递归。
*/
class Solution {
int res = 0;
public int islandPerimeter(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
dfs(grid, i, j);
}
}
}
return res;
}
private void dfs(int[][] grid, int i, int j) {
if ((i < 0 || i >= grid.length)
|| (j < 0 || j >= grid[0].length)
|| grid[i][j] == 0) {
res++;
return;
}
if (grid[i][j] != 1) return;
grid[i][j] = -1;
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
}
}
|
方法2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 迭代判断每个岛屿的四周是否是边界或者海洋
class Solution {
public int islandPerimeter(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
res += getOuter(grid, i, j);
}
}
return res;
}
private int getOuter(int[][] grid, int i, int j) {
int outer = 0;
if (grid[i][j] == 1) {
if (i - 1 < 0 || grid[i - 1][j] == 0) outer++;
if (i + 1 >= grid.length || grid[i + 1][j] == 0) outer++;
if (j + 1 >= grid[0].length || grid[i][j + 1] == 0) outer++;
if (j - 1 < 0 || grid[i][j - 1] == 0) outer++;
}
return outer;
}
}
|
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
/**
每次dfs进行涂色,涂色前初始化当前涂色区域的面积
如果dfs涂完了,说明这个区域遍历完了,更新最大面积。
*/
class Solution {
int maxArea = 0;
int area;
public int maxAreaOfIsland(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
int res = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
area = 0;
dfs(grid, i, j);
maxArea = Math.max(maxArea, area);
}
}
}
return maxArea;
}
private void dfs(int[][] grid, int i, int j) {
if ((i < 0 || i >= grid.length) || (j < 0 || j >= grid[0].length)||
grid[i][j] != 1) return;
area++;
grid[i][j] = -1;
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
}
}
|
动态规划
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class Solution {
/*
dp[i] 表示 [0, i]所能偷到的最大金额数
i如果要偷,则 dp[i-2] + nums[i]
i如果不偷,则 dp[i-1]
*/
public int rob(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
if (n == 1) return nums[0];
if (n == 2) return Math.max(nums[0], nums[1]);
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
dp[i] = Math.max(nums[i] + dp[i - 2], dp[i - 1]);
}
return dp[n - 1];
}
/*
空间优化,由于每次都至于其前两个有关,可以设置两个变量
*/
public int rob(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
if (n == 1) return nums[0];
int first = nums[0], second = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
int third = Math.max(first + nums[i], second);
first = second;
second = third;
}
return second;
}
}
|
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n == 1) {
return nums[0];
} else if (n == 2) {
return Math.max(nums[0], nums[1]);
}
return Math.max(rob_range(nums, 0, n - 2), rob_range(nums, 1, n - 1));
}
public int rob_range(int[] nums, int start, int end) {
int first = nums[start], second = Math.max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
return second;
}
}
|
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int rob(TreeNode root) {
//动态规划
//思路:
//定义一个数组res,长度为2,res[0]表示不抢该节点可获得最大值,res[1]表示抢劫该节点可获得最大值
//方法helper(r)意为:在以r为根节点的树中,返回抢劫根节点与不抢劫根节点可获得的最大值
//执行用时 0ms
int[] res = helper(root);
return Math.max(res[0],res[1]);
}
public int[] helper(TreeNode r){
if(r == null) return new int[2];//边界条件,r为null时,跳出
int[] left = helper(r.left);//对于以r.left为根的树,计算抢劫根节点(r.left)与不抢劫根节点可获得最大金额. left[0]则为不抢r.left可获得的最大金额,left[1]则为抢劫r.left可获得的最大金额 以下right[] 分析同理
int[] right = helper(r.right);
int[] res = new int[2];
res[0] = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);//计算不抢劫当前根节点可获得的最大金额(那么其左右子树可以随便抢)
res[1] = r.val + left[0] + right[0];//计算若抢劫根节点可获得的最大金额(此时,其左右子树的根节点不能被抢)
return res;
}
}
|
子序列系列
公共子序列:由于子序列可以不连续,所以最后一个不相等,可以用前面的来匹配。遍历更新即可,最后返回dp结果。
公共子数组:由于数组要连续,所以最后一个不相等,那么一定匹配不了。遍历要记录每个dp结果,最后返回res。
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// dp
class Solution {
public int lengthOfLIS(int[] nums) {
// dp[i] 表示以i结束的最长递增子序列的长度
// 0 1 2 ... i - 1 i
int n = nums.length;
int[] dp = new int[n];
for (int i = 0; i < n; i++) {
dp[i] = 1;
}
int res = 1;
for (int i = 1; i < n; i++) {
for (int j = i - 1; j >= 0; j--) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], 1 + dp[j]);
res = Math.max(res, dp[i]);
}
}
}
return res;
}
}
|
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public int findLengthOfLCIS(int[] nums) {
// dp[i]表示以nums[i]结尾的最长连续递增子序列的长度
int n = nums.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) {
dp[i] = 1 + dp[i - 1];
res = Math.max(res, dp[i]);
}
}
return res;
}
}
|
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
int[][] dp = new int[len1 + 1][len2 + 1];
int res = 0;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = 0;
}
res = Math.max(res, dp[i][j]);
}
}
return res;
}
}
|
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1 = text1.length(), len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[len1][len2];
}
}
|
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
// 等价于两个字符串的最长公共子序列
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
|
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// 双指针
class Solution {
public boolean isSubsequence(String s, String t) {
int i = 0, j = 0;
while (i < s.length() && j < t.length()) {
if (s.charAt(i) == t.charAt(j)) {
i++;
j++;
} else {
j++;
}
}
return i == s.length();
}
}
// dp
class Solution {
public boolean isSubsequence(String s, String t) {
// 转换为s和t的最长公共子序列长度是否为s的长度
int len1 = s.length(), len2 = t.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return len1 == dp[len1][len2];
}
}
|
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int numDistinct(String s, String t) {
// dp[i][j]表示使用s中前i个字符生成的子序列在t的前j个字符中进行匹配匹配成功的不同种数
int len1 = s.length(), len2 = t.length();
int[][] dp = new int[len1 + 1][len2 + 1];
// 对于s中前i个字符,可以删除所有字符然后和t中的前0个字符即空字符串匹配
for (int i = 0; i <= len1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
// 子序列可以匹配该字符也可以不匹配该字符
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
// 子序列匹配不了该字符,不匹配了,试试前面的
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[len1][len2];
}
}
|
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int minDistance(String word1, String word2) {
// dp[i][j]表示word1前i个字符可以和word2中前j个字符相同所需要的操作数
int len1 = word1.length(), len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 0; i <= len1; i++) {
dp[i][0] = i;
}
for (int j = 0; j <= len2; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(2 + dp[i - 1][j - 1], Math.min(1 + dp[i - 1][j], 1 + dp[i][j - 1]));
}
}
}
return dp[len1][len2];
}
}
|
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public int minDistance(String word1, String word2) {
// dp[i][j]表示word1前i个字符可以和word2中前j个字符相同所需要的操作数
// i \in [0, m], j \in [0, n]
// 转移方程:
// dp[i-1][j] + 1次删除word1的最后一个元素
// dp[i][j-1] + 1次添加word2的最后一个元素
// dp[i-1][j-1] + 0次(如果word1,word2最后一个字符相同)
// dp[i-1][j-1] + 1次替换word1中最后一个字符为word2中最后一个字符
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int j = 0; j < n + 1; j++) {
dp[0][j] = j;
}
for (int i = 0; i < m + 1; i++) {
dp[i][0] = i;
}
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = Math.min(Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1), dp[i - 1][j - 1]);
} else {
dp[i][j] = Math.min(Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1), dp[i - 1][j - 1] + 1);
}
}
}
return dp[m][n];
}
}
|
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
// dp
class Solution {
public int countSubstrings(String s) {
int res = 0;
int len = s.length();
boolean[][] dp = new boolean[len][len];
// s[i] == s[j] && dp[i + 1][j - 1] → dp[i][j]
// 从左下角开始往右上角进行状态转移
for (int i = len - 1; i >= 0; i--) {
for (int j = i; j < len; j++) {
// [i, j], j - i + 1 <= 3
if (s.charAt(i) == s.charAt(j) && (j - i + 1 <= 3 || dp[i + 1][j - 1])) {
dp[i][j] = true;
res++;
}
}
}
return res;
}
}
// 中心扩展
class Solution {
int res = 0;
public int countSubstrings(String s) {
for (int i = 0; i < s.length(); i++) {
count(i, i, s);
count(i, i + 1, s);
}
return res;
}
private void count(int left, int right, String s) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
res++;
left--;
right++;
}
}
}
|
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public int longestPalindromeSubseq(String s) {
// dp[i][j]表示[i, j]这个范围最长回文子序列的长度
int res = 0, len = s.length();
int[][] dp = new int[len][len];
for (int i = len - 1; i >= 0; i--) {
for (int j = i; j < len; j++) {
// [i, j] cnt = j - i + 1
if (j - i + 1 == 1) {
dp[i][j] = 1;
} else if (j - i + 1 == 2) {
dp[i][j] = (s.charAt(i) == s.charAt(j) ? 2 : 1);
} else {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = 2 + dp[i + 1][j - 1];
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
res = Math.max(res, dp[i][j]);
}
}
return res;
}
}
|
股票问题
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[] dp = new int[2];
dp[0] = 0;
dp[1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[0] = Math.max(dp[0], dp[1] + prices[i]);
dp[1] = Math.max(dp[1], -prices[i]);
}
return dp[0];
}
}
|
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int maxProfit_1(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
public int maxProfit(int[] prices) {
int n = prices.length;
int no_socket = 0, own_socket = -prices[0];
for (int i = 1; i < n; i++) {
no_socket = Math.max(no_socket, own_socket + prices[i]);
own_socket = Math.max(own_socket, no_socket - prices[i]);
}
return no_socket;
}
}
|
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
// 第i天不持股,i-1天可以是不持股,也可以是持股然后第i天卖了
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
// 第i天持股,
// i-1天可以是持股
// i-1天不持股然后第i天买入
// i-1天不持股的利润可以直接看i-2天的利润
dp[i][1] = Math.max(dp[i - 1][1], (i >= 2 ? dp[i - 2][0] : 0) - prices[i]);
}
return dp[n - 1][0];
}
}
|
完全背包
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Solution {
public int coinChange(int[] coins, int amount) {
// 完全背包问题
// 背包容量amount,物品集合为coins
// 选择最少的物品放满背包
// dp[i][j]表示用前i个物品装满背包j所需最少的物品数
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= amount; j++) {
if (j == 0) {
dp[i][j] = 0;
} else {
dp[i][j] = amount + 1;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= amount; j++) {
if (coins[i - 1] > j) { // 当前物品太大了放不下
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.min(dp[i - 1][j], 1 + dp[i][j - coins[i - 1]]);
}
}
}
return dp[n][amount] == amount + 1 ? -1 : dp[n][amount];
}
}
class Solution {
public int coinChange(int[] coins, int amount) {
int n = coins.length;
int[] dp = new int[amount + 1];
for (int j = 1; j <= amount; j++) {
dp[j] = amount + 1;
}
for (int i = 1; i <= n; i++) {
for (int j = coins[i - 1]; j <= amount; j++) {
// for (int j = amount; j >= coins[i - 1]; j--) {
// 因为 dp[j - coins[i - 1]]在前面,因此更新dp[j]之前要先得到dp[j - coins[i - 1]] 的值,也就是说要从左到右进行遍历
dp[j] = Math.min(dp[j], 1 + dp[j - coins[i - 1]]);
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
}
|
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
// 转换为完全背包问题
// 物品集coins,背包容积 amount
// dp[i][j]表示用前i个物品塞满背包可以产生的组合数
// 最后返回dp[n][amount]
int[][] dp = new int[n + 1][amount + 1];
// 对于第0行:用0个物品塞背包,组合数肯定为0
// 对于第0列:用i个物品塞背包,组合数也为0
// 直接从(1, 1)遍历
for (int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= amount; j++) {
if (coins[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
}
}
}
return dp[n][amount];
}
}
class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = coins[i - 1]; j <= amount; j++) {
dp[j] = dp[j] + dp[j - coins[i - 1]];
}
}
return dp[amount];
}
}
|
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public int combinationSum4(int[] nums, int target) {
// 使用前i种数字放满容量j的背包的组合数
// 本题与「完全背包求方案数」问题的差别在于:选择方案中的不同的物品顺序代表不同方案。
int n = nums.length;
int[][] dp = new int[n + 1][target + 1];
for (int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= target; j++) {
// 此处选择可以任意选择得到不同的排列
for (int k = i; k >= 1; k--) {
if (nums[k - 1] <= j) {
dp[i][j] += dp[i][j - nums[k - 1]];
}
}
}
}
return dp[n][target];
}
}
|
01背包
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length;
int sum = 0;
for (int num : nums) {
sum += num;
}
if (sum % 2 == 1) {
return false;
}
int target = sum / 2;
boolean[][] dp = new boolean[n + 1][target + 1];
for (int i = 0; i <= n; i++) {
dp[i][0] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= target; j++) {
if (nums[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][target];
}
}
|
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎;
- 如果
x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public int lastStoneWeightII(int[] stones) {
// 我们要将stones分为两组,让这两组的差值尽量的小
// target = sum / 2
// 那么最好情况就是 一个容量为 target 一个容量为 sum - target
// 我们要做的就是判断使用stones[0:j-1],装到容量为 target 的背包中,能够放入的最大容量
int n = stones.length, sum = 0;
for (int stone : stones) {
sum += stone;
}
int target = sum / 2;
int[][] dp = new int[n][target + 1];
for (int i = 0; i < n; i++) {
dp[i][0] = 0;
}
for (int j = 0; j <= target; j++) {
if (j >= stones[0]) {
dp[0][j] = stones[0];
}
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= target; j++) {
if (stones[i] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], stones[i] + dp[i - 1][j - stones[i]]);
}
}
}
return sum - dp[n - 1][target] - dp[n - 1][target];
}
}
|
给定一个整数数组 nums 和一个正整数 k,找出是否有可能把这个数组分成 k 个非空子集,其总和都相等。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
// 先建立k个容量为sum/k的桶,然后一个一个桶的往里面放数字
class Solution {
public boolean canPartitionKSubsets(int[] nums, int k) {
//因为题目限制条件不用担心溢出
int sum = 0;
for(int i = 0; i < nums.length; i++){
sum += nums[i];
}
if(sum % k != 0){
return false;
}
//求出子集的和
sum = sum / k;
//排序 小的放最前面大的放最后面
Arrays.sort(nums);
//如果子集的和小于数组最大的直接返回false
if(nums[nums.length - 1] > sum){
return false;
}
//建立一个长度为k的桶
int[] arr = new int[k];
//桶的每一个值都是子集的和
Arrays.fill(arr, sum);
//从数组最后一个数开始进行递归
return help(nums, nums.length - 1, arr, k);
}
private boolean help(int[] nums, int cur, int[] arr, int k){
//已经遍历到了-1说明前面的所有数都正好可以放入桶里,那所有桶的值此时都为0,说明找到了结果,返回true
if(cur < 0){
return true;
}
//遍历k个桶
for(int i = 0; i < k; i++){
//如果正好能放下当前的数或者放下当前的数后,还有机会继续放前面的数(剪枝)
if(arr[i] == nums[cur] || (cur > 0 && arr[i] - nums[cur] >= nums[0])){
//放当前的数到桶i里
arr[i] -= nums[cur];
//开始放下一个数
if(help(nums, cur - 1, arr, k)){
return true;
}
//这个数不该放在桶i中
//从桶中拿回当前的数
arr[i] += nums[cur];
}
}
return false;
}
}
|
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// dp[i][j][k] 表示strs前i个字符串使用j个0和k个1所能得到的字符串的最多数量
int len = strs.length;
int[][][] dp = new int[len + 1][m + 1][n + 1];
// 最终返回 dp[len][m][n]
for (int i = 1; i <= len; i++) {
int ones = 0, zeros = 0;
for (char c : strs[i - 1].toCharArray()) {
if (c == '1') ones++;
else zeros++;
}
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if (zeros > j || ones > k) {
dp[i][j][k] = dp[i - 1][j][k];
} else {
dp[i][j][k] = Math.max(dp[i - 1][j][k], 1 + dp[i - 1][j - zeros][k - ones]);
}
}
}
}
return dp[len][m][n];
}
}
// 空间优化
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// dp[i][j][k] 有[0, i]这么多物品,要求其总和0要能放到j中,其总和1要能放到k中,最多能装多少物品
int len = strs.length;
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= len; i++) {
String s = strs[i - 1];
int zeros = 0, ones = 0;
for (char c : s.toCharArray()) {
if (c == '0') zeros++;
else ones++;
}
for (int j = m; j >= zeros; j--) {
for (int k = n; k >= ones; k--) {
dp[j][k] = Math.max(dp[j][k], 1 + dp[j - zeros][k - ones]);
}
}
}
return dp[m][n];
}
}
|
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
-
dfs回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
int res = 0;
public int findTargetSumWays(int[] nums, int target) {
dfs(nums, 0, target, 0);
return res;
}
private void dfs(int[] nums, int begin, int target, int pathSum) {
if (begin == nums.length) {
if (pathSum == target) {
res++;
}
} else {
dfs(nums, begin + 1, target, pathSum + nums[begin]);
dfs(nums, begin + 1, target, pathSum - nums[begin]);
}
}
}
|
``
-
dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// Sum(P) - Sum(N) = target
// Sum(P) - Sum(N) + Sum(P) + Sum(N) = target + Sum
// 2 * Sum(P) = target + Sum
// Sum(P) = (target + Sum) / 2
// 问题转化为数组的子集个数,该子集和为 (target + Sum) / 2
int sum = 0;
for (int num : nums) {
sum += num;
}
// target应当是一个正的偶数
if ((target + sum) % 2 != 0 || (target + sum) < 0) return 0;
target = (target + sum) / 2;
if (target < 0) return 0;
return findTargetNum(nums, target);
}
private int findTargetNum(int[] nums, int target) {
// dp[i][j] 表示用nums中前i个数可以得到的和为target的子集数量
// 返回dp[len][target]
int len = nums.length;
int[][] dp = new int[len + 1][target + 1];
dp[0][0] = 1;
for (int i = 1; i <= len; i++) {
for (int j = 0; j <= target; j++) {
if (nums[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[len][target];
}
}
// 空间优化
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// sum(pos) + sum(neg) = target
// sum(pos) - sum(neg) = sum(nums)
// 2*sum(pos) = target + sum(nums)
// sum(pos) = (target + sum(nums)) / 2
int sum = 0;
for (int num : nums) {
sum += num;
}
if ((target + sum) % 2 != 0 || (target + sum) < 0) return 0;
target = (target + sum) / 2;
// 转化为在[0, n]中找物品组合使得总和为target
int n = nums.length;
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = target; j >= nums[i - 1]; j--) {
dp[j] = dp[j] + dp[j - nums[i - 1]];
}
}
return dp[target];
}
}
|
``
二叉树
二叉树遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
// 前序
// 中序
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode p = root;
while (!stack.isEmpty() || p != null) {
if (p != null) {
stack.push(p);
p = p.left;
} else {
p = stack.pop();
res.add(p.val);
p = p.right;
}
}
return res;
}
}
// 后序
// 层序
|
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
// 以j作为根,左 [1,j-1]共j-1个元素 右 [j+1, i]共i-j个元素
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}
|
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
中序遍历非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null) return true;
long last_val = Long.MIN_VALUE;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode p = root;
while (!stack.isEmpty() || p != null) {
while (p != null) {
stack.push(p);
p = p.left;
}
p = stack.pop();
if (p.val > last_val) {
last_val = p.val;
} else {
return false;
}
p = p.right;
}
return true;
}
}
|
中序遍历递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// 递归版本
class Solution {
// 维护一个全局的最小值变量
long min_val = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if (root == null) return true;
if (!isValidBST(root.left)) return false;
if (root.val <= min_val) return false;
min_val = root.val;
return isValidBST(root.right);
}
}
class Solution {
// 维护一个指向最小值的指针pre
TreeNode pre = null;
public boolean isValidBST(TreeNode root) {
if (root == null) return true;
if (!isValidBST(root.left)) return false;
if (pre != null && root.val <= pre.val) return false;
pre = root;
return isValidBST(root.right);
}
}
|
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public boolean isValidBST(TreeNode root) {
return helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean helper(TreeNode root, long lower, long upper) {
if (root == null) return true;
if (root.val > lower && root.val < upper) {
return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
}
return false;
}
}
|
给定一个二叉树,检查它是否是镜像对称的。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// 递归
class Solution {
public boolean isSymmetric_1(TreeNode root) {
if (root == null) return true;
return helper(root.left, root.right);
}
private boolean helper(TreeNode a, TreeNode b) {
if (a == null && b == null) return true;
if (a == null || b == null || a.val != b.val) return false;
return a.val == b.val && helper(a.left, b.right) && helper(a.right, b.left);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
// 非递归
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root.left);
queue.offer(root.right);
while (!queue.isEmpty()) {
TreeNode a = queue.poll();
TreeNode b = queue.poll();
if (a == null && b == null) continue;
if (a == null || b == null || a.val != b.val) return false;
queue.offer(a.left);
queue.offer(b.right);
queue.offer(a.right);
queue.offer(b.left);
}
return true;
}
}
|
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
Deque<TreeNode> queue = new ArrayDeque<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int cnt = queue.size();
List<Integer> temp = new ArrayList<>();
for (int i =0; i < cnt; i++) {
p = queue.poll();
temp.add(p.val);
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
res.add(temp);
}
return res;
}
}
|
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
1
2
3
4
5
6
7
|
// 递归
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
// 非递归
class Solution {
public int maxDepth(TreeNode root) {
int depth = 0;
if (root == null) return depth;
Deque<TreeNode> queue = new ArrayDeque<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
depth++;
int cnt = queue.size();
for (int i = 0; i < cnt; i++) {
p = queue.poll();
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
}
return depth;
}
}
|
给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return helper(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
}
private TreeNode helper(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if ((preorder_left > preorder_right) || (inorder_left > inorder_right)) return null;
TreeNode root = new TreeNode(preorder[preorder_left]);
int inorder_ind = map.get(preorder[preorder_left]);
int left_subtree_size = inorder_ind - 1 - inorder_left + 1, right_subtree_size = inorder_right - (inorder_ind + 1) + 1;
root.left = helper(preorder, inorder, preorder_left + 1, preorder_left + left_subtree_size, inorder_left, inorder_ind - 1);
root.right = helper(preorder, inorder, preorder_right - right_subtree_size + 1, preorder_right, inorder_ind + 1, inorder_right);
return root;
}
}
|
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
前序遍历非递归,先记录,后展开 O(n) O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public void flatten_1(TreeNode root) {
if (root == null) return;
List<TreeNode> list = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
TreeNode p = root;
while (!stack.isEmpty() || p != null) {
while (p != null) {
list.add(p);
stack.push(p);
p = p.left;
}
p = stack.pop();
p = p.right;
}
for (int i = 1; i < list.size(); i++) {
TreeNode prev = list.get(i - 1), cur = list.get(i);
prev.left = null;
prev.right = cur;
}
}
}
|
前序遍历和展开同步进行 O(n) O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public void flatten_2(TreeNode root) {
if (root == null) return;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode p = root;
stack.push(p);
TreeNode prev = null;
while (!stack.isEmpty()) {
p = stack.pop();
if (prev != null) {
prev.left = null;
prev.right = p;
}
prev = p;
if (p.right != null) {
stack.push(p.right);
}
if (p.left != null) {
stack.push(p.left);
}
}
}
}
|
递归 O(n) O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public void flatten(TreeNode root) {
if(root == null){
return;
}
// 对当前节点的处理
if(root.left != null){
// 找到左子树的最右结点,即root的前驱结点
TreeNode pre = root.left;
while(pre.right != null){
pre = pre.right;
}
pre.right = root.right;
root.right = root.left;
root.left = null;
}
// 任何利用二叉树递归处理问题的算法,归根结底都是对根节点的操作
flatten(root.left);
flatten(root.right);
}
}
|
寻找前驱节点 O(n) O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public void flatten(TreeNode root) {
if (root == null) return;
TreeNode cur = root;
// root
// -> root.left -> ... -> root.left最右边结点(pre)
// -> root.right -> root.right的子树
while (cur != null) {
if (cur.left != null) {
TreeNode next = cur.left;
TreeNode pre = next;
while (pre.right != null) {
pre = pre.right;
}
pre.right = cur.right;
cur.left = null;
cur.right = next;
}
cur = cur.right;
}
}
}
|
难度中等713
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
1
2
3
4
5
6
|
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
|
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
// 层序遍历
class Solution {
public Node connect(Node root) {
if (root == null) return null;
Deque<Node> queue= new LinkedList<>();
queue.offer(root);
root.next = null;
while (!queue.isEmpty()) {
int size = queue.size();
Node dummy = new Node();
for (int i = 0; i < size; i++) {
Node p = queue.poll();
if (p.left != null) {
queue.offer(p.left);
dummy.next = p.left;
dummy = dummy.next;
}
if (p.right != null) {
queue.offer(p.right);
dummy.next = p.right;
dummy = dummy.next;
}
}
dummy.next = null;
}
return root;
}
}
// 递归
class Solution {
public Node connect(Node root) {
if (root == null) return root;
if (root.left != null) {
root.left.next = root.right;
root.right.next = root.next == null ? null : root.next.left;
connect(root.left);
connect(root.right);
}
return root;
}
}
|
翻转一棵二叉树。
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
|
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Solution {
// 递归
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null && right == null) return null;
if (left != null && right != null) return root;
return left == null ? right : left;
}
// 存储每个节点的父节点,求得p的所有父节点也即路径,从p到root,然后从q向上遍历得到第一个p遍历过的节点
// 很慢
public TreeNode lowestCommonAncestor_1(TreeNode root, TreeNode p, TreeNode q) {
Map<Integer, TreeNode> parent = new HashMap<>();
Set<Integer> visited = new HashSet<>();
dfs(root, parent);
while (p != null) {
visited.add(p.val);
p = parent.get(p.val);
}
while (q != null) {
if (visited.contains(q.val)) return q;
q = parent.get(q.val);
}
return null;
}
private void dfs(TreeNode root, Map<Integer, TreeNode> parent) {
if (root.left != null) {
parent.put(root.left.val, root);
dfs(root.left, parent);
}
if (root.right != null) {
parent.put(root.right.val, root);
dfs(root.right, parent);
}
}
}
|
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
return root;
}
public TreeNode lowestCommonAncestor_1(TreeNode root, TreeNode p, TreeNode q) {
while (true) {
if (root.val > p.val && root.val > q.val) {
root = root.left;
} else if (root.val < p.val && root.val < q.val) {
root = root.right;
} else {
return root;
}
}
}
}
|
路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
1
2
3
4
5
6
7
8
9
|
// 递归,递归边界为剩余为0
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) return false;
if (root.left == null && root.right == null && root.val == targetSum) return true;
return hasPathSum(root.left, targetSum - root.val)
|| hasPathSum(root.right, targetSum - root.val);
}
}
|
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// dfs,如果到叶子结点路径和等于target则将当前路径放入结果集中
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
dfs(root, targetSum, path, res);
return res;
}
private void dfs(TreeNode root, int targetSum, List<Integer> path, List<List<Integer>> res) {
if (root == null) return;
path.add(root.val);
targetSum -= root.val;
if (root.left == null && root.right == null && targetSum == 0) {
res.add(new ArrayList<>(path));
}
dfs(root.left, targetSum, path, res);
dfs(root.right, targetSum, path, res);
path.remove(path.size() - 1);
targetSum += root.val;
}
}
|
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
// 对每个结点向下进行dfs,如果路径等于target将结果加1
class Solution {
// 双重递归
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return 0;
int res = rootSum(root, targetSum);
res += pathSum(root.left, targetSum);
res += pathSum(root.right, targetSum);
return res;
}
// 从root往下遍历得到路径和为target的路径数量
private int rootSum(TreeNode root, int targetSum) {
if (root == null) return 0;
int res = 0;
int val = root.val;
if (val == targetSum) res++;
res += rootSum(root.left, targetSum - val);
res += rootSum(root.right, targetSum - val);
return res;
}
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
// 前缀和
class Solution {
Map<Integer, Integer> map = new HashMap<>();
int res = 0;
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return res;
map.put(0, 1);
dfs(root, 0, targetSum);
return res;
}
private void dfs(TreeNode root, int curSum, int targetSum) {
if (root == null) return;
curSum += root.val;
if (map.containsKey(curSum - targetSum)) {
res += map.get(curSum - targetSum);
}
map.put(curSum, map.getOrDefault(curSum, 0) + 1);
dfs(root.left, curSum, targetSum);
dfs(root.right, curSum, targetSum);
map.put(curSum, map.getOrDefault(curSum, 0) - 1);
}
}
|
二叉树路径系列
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
int res = 0;
public int diameterOfBinaryTree(TreeNode root) {
if (root == null) return 0;
getDepth(root);
return res;
}
// 对于每个结点root为中心,计算最长路径,从root往左高度 + 从root往右的高度
// 返回以root为根的树的高度,也就是 max(从root往左高度,从root往右的高度)
private int getDepth(TreeNode root) {
if (root == null) return 0;
int left = root.left == null ? 0 : getDepth(root.left) + 1;
int right = root.right == null ? 0 : getDepth(root.right) + 1;
res = Math.max(res, left + right);
return Math.max(left ,right);
}
}
|
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
int res = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return res;
}
// dfs返回以root为根往一边走所能得到的最大路径
private int dfs(TreeNode root) {
if (root == null) return 0;
int leftSum = Math.max(0, dfs(root.left)); // 如果左右孩子的结果是负数的话就舍弃。
int rightSum = Math.max(0, dfs(root.right));
res = Math.max(res, leftSum + rightSum + root.val);
return Math.max(leftSum, rightSum) + root.val;
}
}
class Solution {
private int pathSum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return pathSum;
}
// dfs(node):表示从node结点开始往某个方向所能抵达路径的最大值
// 那么可以两边都不走,可以从node往左走,可以从node往右走
private int dfs(TreeNode node) {
if (node == null) return 0;
int left = dfs(node.left);
int right = dfs(node.right);
// 当前节点有四个选择:
// 1)独立成线,直接返回自己的值
// 2)跟左子节点合成一条路径
// 3)跟右子节点合成一条路径
int res = Math.max(node.val, node.val + Math.max(left, right));
// 4)以自己为桥梁,跟左、右子节点合并成一条路径
pathSum = Math.max(pathSum, Math.max(res, node.val + left + right));
return res;
}
}
|
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
int res = 0;
public int longestUnivaluePath(TreeNode root) {
if (root == null) return 0;
dfs(root);
return res;
}
private int dfs(TreeNode root) {
if (root == null) return 0;
int left = root.left == null ? 0 : 1 + dfs(root.left);
int right = root.right == null ? 0 : 1 + dfs(root.right);
// 如果当前节点和孩子节点不同值,就把边长重新赋值为0。
if (left > 0 && root.left.val != root.val) {
left = 0;
}
if (right > 0 && root.right.val != root.val) {
right = 0;
}
res = Math.max(res, left + right);
return Math.max(left, right);
}
}
|
树的序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
DFS:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
// 用 # 来表示null结点
// dfs
// serialize 1 2 # # 3 4 5
// deserialize
// 1 | 2 # # | 3 4 5
public static final String NULL_VAL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
return root.val + " " + serialize(root.left) + " " + serialize(root.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
Deque<String> strs = new LinkedList<>(Arrays.asList(data.split(" ")));
return dfs(strs);
}
private TreeNode dfs(Deque<String> strs) {
String str = strs.poll();
if (NULL_VAL.equals(str)) {
return null;
}
TreeNode root = new TreeNode(Integer.parseInt(str));
root.left = dfs(strs);
root.right = dfs(strs);
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
|
BFS:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
// serialize: 层序遍历存储val值,null的记录为特殊字符
// 1 | 2 3 | null null 4 5
// deserialize: 新建一个queue用来做层序遍历,对于pop出来结点如果他有孩子则要将孩子入队继续操作
// 每次获取结点从层序序列中获取
public static final String NULL_VAL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
StringBuilder sb = new StringBuilder();
Deque<TreeNode> queue = new LinkedList<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
p = queue.pop();
if (p != null) {
sb.append(p.val + " ");
queue.offer(p.left);
queue.offer(p.right);
} else {
sb.append(NULL_VAL + " ");
}
}
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if (data.trim() == NULL_VAL) return null;
Deque<String> strs = new LinkedList<>(Arrays.asList(data.split(" ")));
Deque<TreeNode> queue = new LinkedList<>();
TreeNode root = new TreeNode(Integer.parseInt(strs.poll()));
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
String left = strs.poll();
String right = strs.poll();
if (!NULL_VAL.equals(left)) {
node.left = new TreeNode(Integer.parseInt(left));
queue.offer(node.left);
}
if (!NULL_VAL.equals(right)) {
node.right = new TreeNode(Integer.parseInt(right));
queue.offer(node.right);
}
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
|
给定一棵二叉树 root,返回所有重复的子树。
对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
如果两棵树具有相同的结构和相同的结点值,则它们是重复的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public static final String NULL_VAL = "#";
Map<String, Integer> map = new HashMap<>();
List<TreeNode> res = new ArrayList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
serialize(root);
return res;
}
private String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
String str = root.val + " " + serialize(root.left) + " " + serialize(root.right);
map.put(str, map.getOrDefault(str, 0) + 1);
if (map.get(str) == 2) {
res.add(root);
}
return str;
}
}
|
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化 二叉搜索树 。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。
Solution1: 二叉搜索树也是二叉树,因此可以和 lc297 一样做
Solution2:前序遍历,然后将序列排序得到中序遍历序列,然后根据前序序列+中序序列构造二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public static final String NULL_VAL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
return root.val + " " + serialize(root.left) + " " + serialize(root.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
Deque<String> queue = new LinkedList<>(Arrays.asList(data.split(" ")));
return dfs(queue);
}
private TreeNode dfs(Deque<String> queue) {
String str = queue.poll();
if (NULL_VAL.equals(str)) return null;
TreeNode root = new TreeNode(Integer.parseInt(str));
root.left = dfs(queue);
root.right = dfs(queue);
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// String tree = ser.serialize(root);
// TreeNode ans = deser.deserialize(tree);
// return ans;
|
链表
反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
// 迭代:设置dummy每次新节点进行头插
public ListNode reverseList(ListNode head) {
ListNode dummy = new ListNode();
ListNode cur = head, temp = null;
while (cur != null) {
temp = cur.next;
cur.next = dummy.next;
dummy.next = cur;
cur = temp;
}
return dummy.next;
}
// 递归:
public ListNode reverseList1(ListNode head) {
if (head == null || head.next == null) return head;
ListNode new_head = reverseList1(head.next);
head.next.next = head;
head.next = null;
return new_head;
}
}
|
难度中等1180
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
// 可以把2、3分别头插到4后面,需要定位到1和4,然后在对2、3进行处理
// 也可以把3、4分别头插到1后面,需要定位到1,然后对2、3进行处理,更快
ListNode dummy = new ListNode(0, head);
ListNode pre = dummy;
for (int i = 0; i < left - 1; i++) {
pre = pre.next;
}
ListNode temp = pre.next;
for (int i = 0; i < right - left; i++) {
ListNode cur = temp.next;
temp.next = cur.next;
cur.next = pre.next;
pre.next = cur;
}
return dummy.next;
}
}
|
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummy = new ListNode(0, head);
ListNode pre = dummy, tail = pre;
while (true) {
for (int i = 0; i < 2; i++) {
if (tail != null) {
tail = tail.next;
}
}
if (tail == null) break;
ListNode cur = pre.next;
pre.next = cur.next;
cur.next = tail.next;
tail.next = cur;
pre = cur;
tail = cur;
}
return dummy.next;
}
}
|
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 每个子序列,使每个最前面的结点尾插到该序列当前tail后面,tail维持不动
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode dummy = new ListNode(0, head);
ListNode pre = dummy, tail = dummy;
while (true) {
for (int i = 0; i < k; i++) {
if (tail != null) {
tail = tail.next;
}
}
if (tail == null) break;
ListNode curHead = pre.next;
while (pre.next != tail) {
ListNode cur = pre.next; // 取出操作的结点
pre.next = cur.next; // 断链
cur.next = tail.next; // 尾插到tail后面
tail.next = cur;
}
pre = curHead;
tail = curHead;
}
return dummy.next;
}
}
|
其他
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode rotateRight(ListNode head, int k) {
if (head == null || head.next == null || k == 0) return head;
ListNode dummy = new ListNode(0, head);
ListNode pre = dummy;
int len = 0;
while (pre.next != null) {
pre = pre.next;
len++;
}
ListNode tail = pre;
pre = dummy;
for (int i = 0; i < len - k % len; i++) {
ListNode cur = pre.next;
pre.next = cur.next;
cur.next = tail.next;
tail.next = cur;
tail = cur;
}
return dummy.next;
}
}
|
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode dummy = new ListNode(0);
ListNode pre = dummy;
ListNode cur = head, tail = head;
while (cur != null) {
while (tail != null && tail.val == cur.val) {
tail = tail.next;
}
// 如果没有相同的 1 2 此时cur指向1,tail指向2
// 如果有相同的 1 1 2,此时cur指向1,tail指向2
// 通过 cur.next == tail 判断是否cur是否重复
if (cur.next == tail) {
pre.next = cur;
pre = cur;
} else {
pre.next = tail;
}
cur = tail;
}
return dummy.next;
}
}
|
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) return false;
ListNode slow = head, fast = head;
// 由于fast在slow前面所以只要判断fast是否为空就可以,不然就是 slow != null && fast != null && fast.next != null
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
return true;
}
}
return false;
}
}
|
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
概括一下:
根据:
f = 2s (快指针每次2步,路程刚好2倍)
f = s + nb (相遇时,刚好多走了n圈)
推出:s = nb
从head结点走到入环点需要走 : a + nb, 而slow已经走了nb,那么slow再走a步就是入环点了。
如何知道slow刚好走了a步? 从head开始,和slow指针一起走,相遇时刚好就是a步
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) return null;
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
while (head != slow) {
head = head.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
}
|
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
进阶:
- 你可以在
O(nlogn) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
class Solution {
// // 自底向上归并排序,O(1)空间复杂度,O(nlgn)时间复杂度
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) return head;
int len = 0;
ListNode p = head;
while (p != null) {
len++;
p = p.next;
}
ListNode dummy = new ListNode(0, head);
for (int sub_len = 1; sub_len < len; sub_len <<= 1) {
ListNode prev = dummy, cur = head;
// sub_len sub_len的起点为cur
// prev sub_len sub_len 重新赋值prev
while (cur != null) {
ListNode first = cur;
for (int i = 0; i < sub_len - 1 && cur != null && cur.next != null; i++) {
cur = cur.next;
}
ListNode second = cur.next;
cur.next = null;
cur = second;
for (int i = 0; i < sub_len - 1 && cur != null && cur.next != null; i++) {
cur = cur.next;
}
ListNode third = null;
// 这个时候cur可能已经没了
if (cur != null) {
third = cur.next;
cur.next = null;
}
ListNode merged = merge(first, second);
prev.next = merged;
while (prev.next != null) {
prev = prev.next;
}
cur = third;
}
}
return dummy.next;
}
// 自顶向下归并排序,O(lgn)空间复杂度,O(nlgn)时间复杂度
public ListNode sortList (ListNode head) {
if (head == null || head.next == null) return head;
return mergeSort(head);
}
private ListNode mergeSort (ListNode head) {
if (head == null || head.next == null) return head;
ListNode prev = new ListNode(0, head);
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
prev = prev.next;
slow = slow.next;
fast = fast.next.next;
}
prev.next = null;
ListNode left = mergeSort(head);
ListNode right = mergeSort(slow);
return merge(left, right);
}
private ListNode merge(ListNode a, ListNode b) {
ListNode dummy = new ListNode();
ListNode p = dummy;
while (a != null && b != null) {
if (a.val < b.val) {
p.next = a;
a = a.next;
} else {
p.next = b;
b = b.next;
}
p = p.next;
}
if (a != null) {
p.next = a;
}
if (b != null) {
p.next = b;
}
return dummy.next;
}
}
|
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
// 通过计算长度差,让较长的先走这个差值,然后一起走,第一次指针指向相同则返回
// 时间复杂度:O(m+n)
// 空间复杂度:O(1)
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode dummyA = new ListNode(0, headA), dummyB = new ListNode(0, headB);
ListNode pA = dummyA, pB = dummyB;
while (pA.next != null && pB.next != null) {
pA = pA.next;
pB = pB.next;
}
if (pA.next == null) {
ListNode temp = pA;
pA = pB;
pB = temp;
ListNode temp_dummy = dummyA;
dummyA = dummyB;
dummyB = temp_dummy;
}
int cnt = 0;
while (pA.next != null) {
pA = pA.next;
cnt++;
}
for (int i = 0; i < cnt; i++) {
dummyA = dummyA.next;
}
while (dummyA != dummyB) {
dummyA = dummyA.next;
dummyB = dummyB.next;
}
return dummyA;
}
// 遍历一个链表将节点存入hashset,然后遍历另一个链表,遍历查看是否在集合中,在的话返回
// 时间复杂度:O(m+n)
// 空间复杂度:O(m)
public ListNode getIntersectionNode1(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
ListNode p = headA;
while (p != null) {
set.add(p);
p = p.next;
}
p = headB;
while (p != null) {
if (set.contains(p)) {
return p;
}
p = p.next;
}
return null;
}
// A: --------******
// B: ---******
// A+B: --------abcdefg---abcdefg
// B+A: ---abcdefg--------abcdefg
// 遍历完了再遍历另一条链表,第一个相同的则返回
// 时间复杂度:O(m+n)
// 空间复杂度:O(1)
public ListNode getIntersectionNode2(ListNode headA, ListNode headB) {
ListNode pA = headA, pB = headB;
while (pA != pB) {
pA = pA != null ? pA.next : headB;
pB = pB != null ? pB.next : headA;
}
return pA;
}
}
|
其他类型
滑动窗口
覆盖子串问题
https://leetcode-cn.com/problems/minimum-window-substring/solution/tong-su-qie-xiang-xi-de-miao-shu-hua-dong-chuang-k/
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
- 如果
s 中存在这样的子串,我们保证它是唯一的答案。
- 两个map
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Solution {
public String minWindow(String s, String t) {
int begin = 0, len = Integer.MAX_VALUE;
// 维护关于s的滑动窗口, mapS要包含mapT中所有元素
Map<Character, Integer> mapS = new HashMap<>(), mapT = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char ch = t.charAt(i);
mapT.put(ch, mapT.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
while (right < s.length()) {
char ch = s.charAt(right);
right++;
mapS.put(ch, mapS.getOrDefault(ch, 0) + 1);
while (isValid(mapS, mapT)) {
if (right - left < len) {
len = right - left;
begin = left;
}
ch = s.charAt(left);
left++;
mapS.put(ch, mapS.get(ch) - 1);
}
}
return len == Integer.MAX_VALUE ? "" : s.substring(begin, begin + len);
}
private boolean isValid(Map<Character, Integer> mapS, Map<Character, Integer> mapT) {
for (char ch : mapT.keySet()) {
if (!mapS.containsKey(ch) || mapS.get(ch) < mapT.get(ch)) {
return false;
}
}
return true;
}
}
|
- 用cnt,need
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public String minWindow(String s, String t) {
// 用cnt表示t中还有多少个字符没有匹配好,need表示具体的剩余匹配个数
int[] need = new int[128];
int left = 0, right = 0, cnt = t.length();
int min_size = Integer.MAX_VALUE;
String res = "";
for (char c : t.toCharArray()) {
need[c]++;
}
while (right < s.length()) {
char r_char = s.charAt(right);
if (need[r_char] > 0) {
cnt--;
}
need[r_char]--;
if (cnt == 0) {
// 缩减到当前最小窗口
while (need[s.charAt(left)] < 0) {
need[s.charAt(left)]++;
left++;
}
// 判断当前的最小窗口
if ((right - left + 1) < min_size) {
min_size = right - left + 1;
res = s.substring(left, right + 1);
}
// 缩减窗口
char l_char = s.charAt(left);
need[l_char]++;
left++;
cnt++;
}
right++;
}
return res;
}
}
|
难度中等622
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
- 用两个map
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Solution {
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) {
return false;
}
Map<Character, Integer> map1 = new HashMap<>(), map2 = new HashMap<>();
for (int i = 0; i < s1.length(); i++) {
char ch = s1.charAt(i);
map1.put(ch, map1.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
while (right < s2.length()) {
char ch = s2.charAt(right);
right++;
map2.put(ch, map2.getOrDefault(ch, 0) + 1);
while (isValid(map1, map2)) {
if (right - left == s1.length()) {
return true;
}
ch = s2.charAt(left);
left++;
map2.put(ch, map2.get(ch) - 1);
}
}
return false;
}
private boolean isValid(Map<Character, Integer> map1, Map<Character, Integer> map2) {
for (char ch : map1.keySet()) {
if (!map2.containsKey(ch) || map2.get(ch) < map1.get(ch)) {
return false;
}
}
return true;
}
}
|
- 用cnt和need
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) return false;
int[] need = new int[128];
int cnt = s1.length();
for (int i = 0; i < s1.length(); i++) {
need[s1.charAt(i)]++;
}
int l = 0, r = 0;
while (r < s2.length()) {
if (need[s2.charAt(r)] > 0) {
cnt--;
}
need[s2.charAt(r)]--;
if (cnt == 0) {
while (need[s2.charAt(l)] < 0) {
need[s2.charAt(l)]++;
l++;
}
if (r - l + 1 == s1.length()) {
return true;
}
need[s2.charAt(l)]++;
cnt++;
l++;
}
r++;
}
return false;
}
}
|
难度中等828
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
- 用两个map
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
Map<Character, Integer> mapS = new HashMap<>(), mapP = new HashMap<>();
for (int i = 0; i < p.length(); i++) {
char ch = p.charAt(i);
mapP.put(ch, mapP.getOrDefault(ch, 0) + 1);
}
int left = 0, right = 0;
while (right < s.length()) {
char ch = s.charAt(right);
right++;
mapS.put(ch, mapS.getOrDefault(ch, 0) + 1);
while (isValid(mapS, mapP)) {
if (right - left == p.length()) {
res.add(left);
}
ch = s.charAt(left);
left++;
mapS.put(ch, mapS.get(ch) - 1);
}
}
return res;
}
private boolean isValid(Map<Character, Integer> mapS, Map<Character, Integer> mapP) {
for (char ch : mapP.keySet()) {
if (!mapS.containsKey(ch) || mapS.get(ch) < mapP.get(ch)) {
return false;
}
}
return true;
}
}
|
- 用need、cnt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
if (s.length() < p.length()) return res;
int[] need = new int[128];
int cnt = p.length();
for (int i = 0; i < p.length(); i++) {
need[p.charAt(i)]++;
}
int l = 0, r = 0;
while (r < s.length()) {
if (need[s.charAt(r)] > 0) {
cnt--;
}
need[s.charAt(r)]--;
if (cnt == 0) {
while (need[s.charAt(l)] < 0) {
need[s.charAt(l)]++;
l++;
}
if (r - l + 1 == p.length()) {
res.add(l);
}
need[s.charAt(l)]++;
cnt++;
l++;
}
r++;
}
return res;
}
}
|
滑动窗口
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int l = 0, r = 0, sum = 0;
int minSize = Integer.MAX_VALUE;
while (r < nums.length) {
sum += nums[r++];
while (sum >= target) {
minSize = Math.min(minSize, r - 1 - l + 1);
sum -= nums[l++];
}
}
return minSize == Integer.MAX_VALUE ? 0 : minSize;
}
}
|
给定一个字符串 s 和一些 长度相同 的单词 words **。**找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 words 中的单词完全匹配,中间不能有其他字符 ,但不需要考虑 words 中单词串联的顺序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public List<Integer> findSubstring(String s, String[] words) {
// 对于s的一个子区间,这个子区间切成字符串后正好对应words中的元素
List<Integer> res = new ArrayList<>();
int n = words.length, len = words[0].length();
int total = n * len;
Map<String, Integer> wordMap = new HashMap<>();
for (String word : words) {
wordMap.put(word, wordMap.getOrDefault(word, 0) + 1);
}
for (int i = 0; i <= s.length() - total; i++) {
Map<String, Integer> map = new HashMap<>();
String cur = s.substring(i, i + total);
boolean flag = true;
for (int j = 0; j <= n - 1; j++) {
// [0, len] [len, 2len] .... [(n-1)len, nlen]
String temp = cur.substring(j * len, (j + 1) * len);
if (wordMap.containsKey(temp) && map.getOrDefault(temp, 0) < wordMap.get(temp)) {
map.put(temp, map.getOrDefault(temp, 0) + 1);
} else {
flag = false;
break;
}
}
if (flag) res.add(i);
}
return res;
}
}
|
旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int search(int[] nums, int target) {
if (nums == null || nums.length == 0) return -1;
int len = nums.length, left = 0, right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
if (nums[mid] < nums[left]) {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
} else {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
}
}
return nums[left] == target ? left : -1;
}
}
|
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。(可能有重复的值)
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/*
该题与33. 搜索旋转排序数组的区别在于,这题的数组中可能会出现重复元素。
二分查找的本质就是在循环的每一步中考虑排除掉哪些元素,本题在用二分查找时,只有在nums[mid]严格大于或小于左边界时才能判断它左边或右边是升序的,这时可以再根据nums[mid], target与左右边界的大小关系排除掉一半的元素;
当nums[mid]等于左边界时,无法判断是mid的左边还是右边是升序数组,而只能肯定左边界不等于target(因为nums[mid] != target),所以只能排除掉这一个元素,让左边界加一。
*/
class Solution {
public boolean search(int[] nums, int target) {
int len = nums.length, left = 0, right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return true;
if (nums[mid] == nums[left]) {
left++;
} else if (nums[mid] > nums[left]) {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return nums[left] == target;
}
}
|
搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素原先是按升序排列的。若有多个相同元素,返回索引值最小的一个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public int search(int[] arr, int target) {
if (arr[0] == target) return 0;
int left = 0, right = arr.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
while (mid > 0 && arr[mid - 1] == arr[mid]) mid--;
return mid;
}
if (arr[mid] == arr[right]) {
right--;
} else if (arr[mid] < arr[right]) {
if (arr[mid] < target && target <= arr[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
} else {
if (arr[left] <= target && target < arr[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
}
}
return arr[left] == target ? left : -1;
}
}
|
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转
7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public int findMin(int[] nums) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 最后一段是 [l, l+1],此时mid等于l,nums[mid]==nums[l]无法判断较小的在左边还是右边也就是无法进一步缩小区间,如果和右端点比的话,mid等于l+1,nums[l]和nums[l+1]可以判断谁大谁小,也就可以进一步缩小区间
// 同理,要是要搜索旋转数组的最大值,那么就要和左端点比了
if (nums[mid] <= nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
}
}
|
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public int findMin(int[] nums) {
int len = nums.length, left = 0, right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 对于有重复元素的情况,如果等于的话,只能把当前元素排除
if (nums[mid] == nums[right]) {
right--;
} else if (nums[mid] < nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
}
}
|
LRU & LFU
实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:你是否可以在 O(1) 时间复杂度内完成这两种操作?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
class LRUCache {
class Node {
int key, val;
Node next, prev;
public Node(int key, int val) {
this.key = key;
this.val = val;
}
}
class DoubleList {
Node head, tail;
int size;
public int getSize() {
return this.size;
}
public DoubleList() {
head = new Node(0, 0);
tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
size = 0;
}
public void remove(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
size--;
}
public Node removeLast() {
Node last = tail.prev;
remove(last);
return last;
}
public void addFirst(Node node) {
Node p = head, q = head.next;
node.prev = p;
p.next = node;
node.next = q;
q.prev = node;
size++;
}
}
DoubleList doubleList;
Map<Integer, Node> map;
int capacity;
public LRUCache(int capacity) {
doubleList = new DoubleList();
map = new HashMap<>();
this.capacity = capacity;
}
public int get(int key) {
if (!map.containsKey(key)) return -1;
int val = map.get(key).val;
put(key, val);
return val;
}
public void put(int key, int value) {
Node node = new Node(key, value);
if (map.containsKey(key)) {
doubleList.remove(map.get(key));
doubleList.addFirst(node);
map.put(key, node);
} else {
if (doubleList.getSize() == capacity) {
Node last = doubleList.removeLast();
map.remove(last.key);
}
doubleList.addFirst(node);
map.put(key, node);
}
}
}
|
难度困难515
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象int get(int key) - 如果键 key 存在于缓存中,则获取键的值,否则返回 -1 。void put(int key, int value) - 如果键 key 已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量 capacity 时,则应该在插入新项之前,移除最不经常使用的项。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最近最久未使用 的键。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
class LFUCache {
class Node {
int key, value;
int freq = 1;
Node prev, next;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
class DoubleList {
Node head, tail;
public DoubleList() {
head = new Node(0, 0);
tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
}
public void addNode(Node node) {
Node p = head.next;
node.prev = head;
head.next = node;
node.next = p;
p.prev = node;
}
public void removeNode(Node node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
}
Map<Integer, Node> cache; // 存储缓存的内容
Map<Integer, DoubleList> freqMap; // 存储每个频次对应的双向链表
int capacity; // 缓存最大容量
int min; // 存储当前最小频次
public LFUCache(int capacity) {
this.cache = new HashMap<> (capacity);
this.freqMap = new HashMap<>();
this.capacity = capacity;
this.min = 0;
}
public int get(int key) {
if (!cache.containsKey(key)) return -1;
Node node = cache.get(key);
freqInc(node);
return node.value;
}
public void put(int key, int value) {
if (capacity == 0) {
return;
}
if (cache.containsKey(key)) {
Node node = cache.get(key);
node.value = value;
freqInc(node);
} else {
if (cache.size() == capacity) {
DoubleList minFreqList = freqMap.get(min);
Node last = minFreqList.tail.prev;
minFreqList.removeNode(last);
cache.remove(last.key);
}
Node newNode = new Node(key, value);
if (!freqMap.containsKey(1)) {
freqMap.put(1, new DoubleList());
}
DoubleList list = freqMap.get(1);
list.addNode(newNode);
cache.put(key, newNode);
min = 1;
}
}
public void freqInc(Node node) {
// 从原freq对应的链表里移除, 并更新min
int freq = node.freq;
DoubleList list = freqMap.get(freq);
list.removeNode(node);
// 一定要注意这一步判断:移除当前元素后是否要更新minFreq
if (freq == min && list.head.next == list.tail) {
min = freq + 1;
}
// 加入新freq对应的链表
node.freq++;
if (!freqMap.containsKey(freq + 1)) {
freqMap.put(freq + 1, new DoubleList());
}
freqMap.get(freq + 1).addNode(node);
}
}
|
二分模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
// 查找第一个值等于给定值的元素
private int firstEquals(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l < r) {
int mid = l + ((r - l) >> 1);
if (arr[mid] < target) l = mid + 1;
else r = mid; // 收缩右边界不影响 first equals
}
if (arr[l] == target && (l == 0 || arr[l - 1] < target)) return l;
return -1;
}
// 查找最后一个值等于给定值的元素
private int lastEquals(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l < r) {
int mid = l + ((r - l + 1) >> 1);
if (arr[mid] > target) r = mid - 1;
else l = mid; // 收缩左边界不影响 last equals
}
if (arr[l] == target && (l == arr.length - 1 || arr[l + 1] > target)) return l;
return -1;
}
// 查找第一个大于等于给定值的元素
private int firstLargeOrEquals(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l < r) {
int mid = l + ((r - l) >> 1);
if (arr[mid] < target) l = mid + 1;
else r = mid; // 收缩右边界不影响 first equals
}
if (arr[l] >= target && (l == 0 || arr[l - 1] < target)) return l; // >=
return -1;
}
// 查找最后一个小于等于给定值的元素
private int lastLessOrEquals(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l < r) {
int mid = l + ((r - l + 1) >> 1);
if (arr[mid] > target) r = mid - 1;
else l = mid; // 收缩左边界不影响 last equals
}
if (arr[l] <= target && (l == arr.length - 1 || arr[l + 1] > target)) return l; // <=
return -1;
}
|
拓扑排序
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
参考:
总结:拓扑排序问题
根据依赖关系,构建邻接表、入度数组。
选取入度为 0 的数据,根据邻接表,减小依赖它的数据指向的入度。
找出入度变为 0 的数据,重复第 2 步。
直至所有数据的入度为 0,得到排序,如果还有数据的入度不为 0,说明图中存在环。
作者:xiao_ben_zhu
链接:https://leetcode-cn.com/problems/course-schedule/solution/bao-mu-shi-ti-jie-shou-ba-shou-da-tong-tuo-bu-pai-/
来源:力扣(LeetCode)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] indegree = new int[numCourses];
Map<Integer, List<Integer>> map = new HashMap<>();
for (int[] prerequisite : prerequisites) {
int head = prerequisite[1], tail = prerequisite[0];
indegree[tail]++;
if (!map.containsKey(head)) map.put(head, new ArrayList<>());
map.get(head).add(tail);
}
Deque<Integer> queue = new LinkedList<>();
for (int i = 0; i < indegree.length; i++) {
if (indegree[i] == 0) {
queue.offer(i);
}
}
int cnt = 0;
while (!queue.isEmpty()) {
int head = queue.poll();
cnt++;
if (map.containsKey(head)) {
List<Integer> tails = map.get(head);
for (int tail : tails) {
indegree[tail]--;
if (indegree[tail] == 0) {
queue.offer(tail);
}
}
}
}
return cnt == numCourses;
}
}
// dfs
class Solution {
// 对每个结点开始dfs,维护flags数组
// flags[i] == 0,没有被dfs遍历过
// flags[i] == -1,被其他结点开始的dfs遍历过
// flags[i] == 1,被当前结点开始的dfs遍历过
public boolean canFinish(int numCourses, int[][] prerequisites) {
Map<Integer, List<Integer>> map = new HashMap<>();
int[] flags = new int[numCourses];
for (int[] prerequisite : prerequisites) {
int head = prerequisite[1], tail = prerequisite[0];
if (!map.containsKey(head)) map.put(head, new ArrayList<>());
map.get(head).add(tail);
}
for (int i = 0; i < numCourses; i++) {
if (!dfs(map, i, flags)) return false;
}
return true;
}
private boolean dfs(Map<Integer, List<Integer>> map, int i, int[] flags) {
if (flags[i] == -1) return true;
if (flags[i] == 1) return false;
flags[i] = 1;
if (map.containsKey(i)) {
List<Integer> tails = map.get(i);
for (int tail : tails) {
if (!dfs(map, tail, flags)) return false;
}
}
flags[i] = -1;
return true;
}
}
// 如果不知道课程的号码
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
Map<Integer, Integer> indegrees = new HashMap<>(); // 记录入度
Map<Integer, List<Integer>> map = new HashMap<>(); // 记录图
Set<Integer> courses = new HashSet<>(); // 记录课程号
for (int[] prerequisite : prerequisites) {
int head = prerequisite[1], tail = prerequisite[0];
indegrees.put(tail, indegrees.getOrDefault(tail, 0) + 1);
indegrees.put(head, indegrees.getOrDefault(head, 0)); // 注意也要将head加入防止找不到head
courses.add(head);
courses.add(tail);
if (!map.containsKey(head)) map.put(head, new ArrayList<>());
map.get(head).add(tail);
}
Deque<Integer> queue = new LinkedList<>();
for (int tail : indegrees.keySet()) {
if (indegrees.get(tail) == 0) {
queue.offer(tail);
}
}
int cnt = 0;
while (!queue.isEmpty()) {
int head = queue.poll();
cnt++;
if (map.containsKey(head)) {
List<Integer> tails = map.get(head);
for (int tail : tails) {
indegrees.put(tail, indegrees.get(tail) - 1);
if (indegrees.get(tail) == 0) {
queue.offer(tail);
}
}
}
}
return cnt == courses.size();
}
}
|
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] res = new int[numCourses];
int ind = 0;
int[] indegree = new int[numCourses]; // value -> indegree
Map<Integer, List<Integer>> map = new HashMap<>(); // value -> tails from value
for (int[] prerequisite : prerequisites) {
int head = prerequisite[1], tail = prerequisite[0];
indegree[tail]++;
if (!map.containsKey(head)) map.put(head, new ArrayList<>());
map.get(head).add(tail);
}
Deque<Integer> queue = new LinkedList<>();
for (int i = 0; i < indegree.length; i++) {
if (indegree[i] == 0) {
queue.offer(i);
}
}
while(!queue.isEmpty()) {
int head = queue.poll();
res[ind++] = head;
if (map.containsKey(head)) {
List<Integer> tails = map.get(head);
for (int tail : tails) {
indegree[tail]--;
if (indegree[tail] == 0) {
queue.offer(tail);
}
}
}
}
return ind == numCourses ? res : new int[0];
}
}
|
重复数相关
找出数组中重复的数字。在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int findRepeatNumber(int[] nums) {
// 限定了数字的范围,因此可以原地哈希,不用额外开哈希表
for (int i = 0; i < nums.length; i++) {
while (nums[i] != i) {
if (nums[i] == nums[nums[i]]) {
return nums[i];
}
swap(nums, i, nums[i]);
}
}
return -1;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
|
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public int findDuplicate(int[] nums) {
// 范围都在 [1, n],就算都不同,那么就会出现有两个不同的下标,他们位置上的元素相同,建立从下标到数字的映射,将问题转化为链表有环的问题
int slow = 0, fast = 0;
while (true) {
slow = nums[slow];
fast = nums[nums[fast]];
if (slow == fast) {
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
}
}
}
|
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public int singleNumber(int[] nums) {
// a ^ 0 = a, a ^ a = 0
int res = 0;
for (int num : nums) {
res ^= num;
}
return res;
}
}
|
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int singleNumber(int[] nums) {
// 每一位上相加,如果该位上是3的倍数,则结果该位为0,否则为1
int[] digits = new int[32];
for (int num : nums) {
for (int i = 0; i < 32; i++) {
digits[i] += (num & 1);
num >>= 1;
}
}
int res = 0;
for (int i = 31; i >= 0; i--) {
res <<= 1;
if (digits[i] % 3 != 0) {
res = (res | 1); // 将该位数字置为1
}
}
return res;
}
}
|
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int[] singleNumber(int[] nums) {
// a ^ b = x
// a和b至少有一位是不一样的,找出这个位置,然后对于数组中的每个数,根据这一位是否为1分为两组,两组分别异或,得到两组最后结果
int x = 0;
for (int num : nums) {
x ^= num;
}
int idx = 0;
while ((x & 1) == 0) {
x >>= 1;
idx++;
}
int a = 0, b = 0;
for (int num : nums) {
if (((num >> idx) & 1) == 0) {
a ^= num;
} else {
b ^= num;
}
}
return new int[]{a, b};
}
}
|
并查集
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程 equations[i] 的长度为 4,并采用两种不同的形式之一:"a==b" 或 "a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。
只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回 true,否则返回 false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public boolean equationsPossible(String[] equations) {
int[] parent = new int[26];
for (int i = 0; i < 26; i++) {
parent[i] = i;
}
for (String equation : equations) {
if ("==".equals(equation.substring(1, 3))) {
int idx1 = equation.charAt(0) - 'a', idx2 = equation.charAt(3) - 'a';
merge(parent, idx1, idx2);
}
}
for (String equation : equations) {
if ("!=".equals(equation.substring(1, 3))) {
int idx1 = equation.charAt(0) - 'a', idx2 = equation.charAt(3) - 'a';
if (find(parent, idx1) == find(parent, idx2)) return false;
}
}
return true;
}
private void merge(int[] parent, int idx1, int idx2) {
parent[find(parent, idx1)] = find(parent, idx2);
}
private int find(int[] parent, int idx) {
if (parent[idx] == idx) {
return idx;
} else {
return find(parent, parent[idx]);
}
}
}
|
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
**注意:**输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
int n_var = 0;
Map<String, Integer> variables = new HashMap<>();
int n = equations.size();
for (List<String> equation : equations) {
if (!variables.containsKey(equation.get(0))) {
variables.put(equation.get(0), n_var++);
}
if (!variables.containsKey(equation.get(1))) {
variables.put(equation.get(1), n_var++);
}
}
int[] f = new int[n_var];
double[] w = new double[n_var];
for (int i = 0; i < n_var; i++) {
f[i] = i;
w[i] = 1.0;
}
for (int i = 0; i < n; i++) {
int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));
merge(f, w, va, vb, values[i]);
}
int queriesCount = queries.size();
double[] ret = new double[queriesCount];
for (int i = 0; i < queriesCount; i++) {
List<String> query = queries.get(i);
double result = -1.0;
if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {
int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));
int fa = find(f, w, ia), fb = find(f, w, ib);
if (fa == fb) {
result = w[ia] / w[ib];
}
}
ret[i] = result;
}
return ret;
}
private void merge(int[] f, double[] w, int x, int y, double val) {
int fx = find(f, w, x);
int fy = find(f, w, y);
f[fx] = fy;
w[fx] = val * w[y] / w[x];
}
private int find(int[] f, double[] w, int x) {
if (f[x] != x) {
int father = find(f, w, f[x]);
w[x] = w[x] * w[f[x]];
f[x] = father;
}
return f[x];
}
}
|
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int[][] reconstructQueue(int[][] people) {
// 按照身高降序 K升序排序
Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]);
List<int[]> res = new ArrayList<>();
// K值定义为 排在h前面且身高大于或等于h的人数
// 因为从身高降序开始插入,此时所有人身高都大于等于h
// 因此K值即为需要插入的位置
for (int[] arr : people) {
res.add(arr[1], arr);
}
return res.toArray(new int[res.size()][]);
}
}
|
其他题解
主要
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map = new HashMap<>();
int ans = 0;
for (int left = 0, right = 0; right < s.length(); right++) {
if (map.containsKey(s.charAt(right))) {
left = Math.max(left, map.get(s.charAt(right)) + 1);
}
ans = Math.max(ans, right - left + 1);
map.put(s.charAt(right), right);
}
return ans;
}
}
|
优化:用数组代替map,map的作用就是记录当前这个窗口中什么时候出现了这个新的重复的元素,那么每次记录下每个元素的下标就可以了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public int lengthOfLongestSubstring(String s) {
int[] last = new int[128];
for (int i = 0; i < 128; i++) {
last[i] = -1;
}
int ans = 0;
for (int left = 0, right = 0; right < s.length(); right++) {
if (last[s.charAt(right)] != -1) {
left = Math.max(left, last[s.charAt(right)] + 1);
}
ans = Math.max(ans, right - left + 1);
last[s.charAt(right)] = right;
}
return ans;
}
}
|
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
Solution1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/*这道题让我们求两个有序数组的中位数,而且限制了时间复杂度为O(log (m+n)),看到这个时间复杂度,自然而然的想到了应该使用二分查找法来求解。那么回顾一下中位数的定义,如果某个有序数组长度是奇数,那么其中位数就是最中间那个,如果是偶数,那么就是最中间两个数字的平均值。这里对于两个有序数组也是一样的,假设两个有序数组的长度分别为m和n,由于两个数组长度之和 m+n 的奇偶不确定,因此需要分情况来讨论,对于奇数的情况,直接找到最中间的数即可,偶数的话需要求最中间两个数的平均值。为了简化代码,不分情况讨论,我们使用一个小trick,我们分别找第 (m+n+1) / 2 个,和 (m+n+2) / 2 个,然后求其平均值即可,这对奇偶数均适用。加入 m+n 为奇数的话,那么其实 (m+n+1) / 2 和 (m+n+2) / 2 的值相等,相当于两个相同的数字相加再除以2,还是其本身。
这里我们需要定义一个函数来在两个有序数组中找到第K个元素,下面重点来看如何实现找到第K个元素。首先,为了避免产生新的数组从而增加时间复杂度,我们使用两个变量i和j分别来标记数组nums1和nums2的起始位置。然后来处理一些边界问题,比如当某一个数组的起始位置大于等于其数组长度时,说明其所有数字均已经被淘汰了,相当于一个空数组了,那么实际上就变成了在另一个数组中找数字,直接就可以找出来了。还有就是如果K=1的话,那么我们只要比较nums1和nums2的起始位置i和j上的数字就可以了。难点就在于一般的情况怎么处理?因为我们需要在两个有序数组中找到第K个元素,为了加快搜索的速度,我们要使用二分法,对K二分,意思是我们需要分别在nums1和nums2中查找第K/2个元素,注意这里由于两个数组的长度不定,所以有可能某个数组没有第K/2个数字,所以我们需要先检查一下,数组中到底存不存在第K/2个数字,如果存在就取出来,否则就赋值上一个整型最大值。如果某个数组没有第K/2个数字,那么我们就淘汰另一个数字的前K/2个数字即可。有没有可能两个数组都不存在第K/2个数字呢,这道题里是不可能的,因为我们的K不是任意给的,而是给的m+n的中间值,所以必定至少会有一个数组是存在第K/2个数字的。最后就是二分法的核心啦,比较这两个数组的第K/2小的数字midVal1和midVal2的大小,如果第一个数组的第K/2个数字小的话,那么说明我们要找的数字肯定不在nums1中的前K/2个数字,所以我们可以将其淘汰,将nums1的起始位置向后移动K/2个,并且此时的K也自减去K/2,调用递归。反之,我们淘汰nums2中的前K/2个数字,并将nums2的起始位置向后移动K/2个,并且此时的K也自减去K/2,调用递归即可。
转自评论区:作者 Wait想念
*/
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
int left = (len1 + len2 + 1) / 2;
int right = (len1 + len2 + 2) / 2;
return (findKthSmallest(nums1, 0, nums2, 0, left) + findKthSmallest(nums1, 0, nums2, 0, right)) / 2.0;
}
// 从nums1的i下标开始,从nums的下标j开始,找到以这两个下标开始的子数组的第k个数(从小到大)
private int findKthSmallest(int[] nums1, int i, int[] nums2, int j, int k) {
if (i > nums1.length - 1) return nums2[j + k - 1];
if (j > nums2.length - 1) return nums1[i + k - 1];
if (k == 1) return Math.min(nums1[i], nums2[j]);
int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
if (midVal1 < midVal2) {
// nums1的第k/2个数较小,说明要找的数字肯定不在nums1的前k/2个数中
// 如果nums1没有k/2个元素,说明nums2的前k/2个数都不是所求,可以割掉
// 要割nums2就要使得midVal1较大,因此这种情况可以赋予它一个整型最大值
return findKthSmallest(nums1, i + k / 2, nums2, j, k - k / 2);
} else {
return findKthSmallest(nums1, i, nums2, j + k / 2, k - k / 2);
}
}
}
|
难度简单1894
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public boolean isPalindrome(int x) {
if (x < 0) return false;
int a = x, b = 0;
while (x != 0) {
b = b * 10 + (x % 10);
x /= 10;
}
return a == b;
}
}
|
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
- 读入字符串并丢弃无用的前导空格
- 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
- 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
- 将前面步骤读入的这些数字转换为整数(即,“123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为
0 。必要时更改符号(从步骤 2 开始)。
- 如果整数数超过 32 位有符号整数范围
[−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
- 返回整数作为最终结果。
注意:
- 本题中的空白字符只包括空格字符
' ' 。
- 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int myAtoi(String s) {
int i = 0, n = s.length();
while (i < n && s.charAt(i) == ' ') i++; // 删除前置0
if (i == n) return 0;
boolean isNeg = false; // 判断正负号
if (s.charAt(i) == '-') {
isNeg = true;
i++;
} else if (s.charAt(i) == '+') {
i++;
}
int res = 0; // 计数
while (i < n && s.charAt(i) >= '0' && s.charAt(i) <= '9') {
int digit = s.charAt(i) - '0';
if (res > (Integer.MAX_VALUE - digit) / 10) { // 如果超过了提前返回
return isNeg ? Integer.MIN_VALUE : Integer.MAX_VALUE;
}
res = res * 10 + digit;
i++;
}
return isNeg ? -res : res;
}
}
|
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length(), n = p.length();
// dp[i][j] 表示s的前i个元素是否可以和p的前j个元素进行匹配
boolean[][] dp = new boolean[m+1][n+1];
dp[0][0] = true;
// first column
for (int i = 1; i <= m; i++) {
dp[i][0] = false;
}
// first row
for (int j = 1; j <= n; j++) {
if (j >= 2 && p.charAt(j-1) == '*') {
dp[0][j] = dp[0][j-2];
} else {
dp[0][j] = false;
}
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(p.charAt(j-1) != '*'){
dp[i][j] = (s.charAt(i-1) == p.charAt(j-1) || p.charAt(j-1) == '.') && dp[i-1][j-1];
}
else{
if(s.charAt(i-1) == p.charAt(j-2) || p.charAt(j-2) == '.'){
dp[i][j] = dp[i][j-1] || dp[i-1][j];
if(j > 1) dp[i][j] = dp[i][j] || dp[i][j-2];
}
else{
dp[i][j] = dp[i][j-2];
}
}
}
}
return dp[m][n];
}
}
|
难度简单2142
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
String prefix = strs[0];
for (int i = 1; i < strs.length; i++) {
prefix = longestCommonPrefix(prefix, strs[i]);
if (prefix == "") return "";
}
return prefix;
}
private String longestCommonPrefix(String str1, String str2) {
int minLen = Math.min(str1.length(), str2.length());
int i = 0;
while (i < minLen && str1.charAt(i) == str2.charAt(i)) {
i++;
}
return str1.substring(0, i);
}
}
|
难度中等871
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int divide(int dividend, int divisor) {
if (dividend == 0) return 0;
if (dividend == Integer.MIN_VALUE && divisor == -1) {
return Integer.MAX_VALUE;
}
boolean isNegative = (dividend ^ divisor) < 0;
int res = 0;
long a = Math.abs((long) dividend);
long b = Math.abs((long) divisor);
// 100 3
// 100/64<3
// 100/32>=3
// 所以可以先得到32个3
// 将100减去32个3,然后处理剩余的4
for (int i = 31; i >= 0; i--) {
if ((a >> i) >= b) {
res += 1 << i;
a -= b << i;
}
}
return isNegative ? -res : res;
}
}
|
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列(即,组合出下一个更大的整数)。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须** 原地 **修改,只允许使用额外常数空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public void nextPermutation(int[] nums) {
int len = nums.length;
int i = len - 2;
// 1238 5 764
// 1238 6 754
// 764已经最大了,只能继续看左边的5此时从7下降到5说明肯定可以变大
// 但是不能变的太大,只能找到后面第一个比5大的数字也就是6,将两者交换,得到12386754、
// 将i右边的数字降序换为升序
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = len - 1;
while (j > i && nums[j] <= nums[i]) {
j--;
}
swap(nums, i, j);
}
// [i+1, len-1] reverse
reverse(nums, i + 1, len - 1);
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void reverse(int[] nums, int left, int right) {
while (left < right) {
swap(nums, left, right);
left++;
right--;
}
}
}
|
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int longestValidParentheses(String s) {
int ans = 0;
if (s == null || s.length() == 0) return ans;
// dp[i]表示以i结尾的最长括号子串的长度
// 每次判断 )
//两种情况
// yyyyxxxx()
// yyyy(xxxx),注意(前面的内容也要加入
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i - 2 >= 0 ? dp[i - 2] : 0) + 2;
} else if(i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + 2 + (i - dp[i - 1] >= 2 ? dp[i - dp[i - 1] - 2] : 0);
}
ans = Math.max(ans, dp[i]);
}
}
return ans;
}
}
|
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public int removeDuplicates(int[] nums) {
int slow = 0;
for (int fast = 1; fast < nums.length; fast++) {
if (nums[fast] != nums[slow]) {
nums[++slow] = nums[fast];
}
}
return slow + 1;
}
}
|
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 最多出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public int removeDuplicates(int[] nums) {
int slow = 1;
for (int fast = 2; fast < nums.length; fast++) {
if (nums[fast] != nums[slow - 1]) {
nums[++slow] = nums[fast];
}
}
return slow + 1;
}
}
|
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
Solution1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
/*
对于每个下标为i的地方,我们看这个地方能不能放得下雨水,就是说它左边有没有比它高的,右边有没有比它高的。
对于能放下多少,只要看左边最高的有多高,右边最高的有多高,这两个一左一右最高的形成两个围墙把它围起来,这个地方放的水量就是
如果min(left_max, right_max) - height[i] > 0,则为min(left_max, right_max) - height[i],否则为0
时间复杂度:O(n^2)
空间复杂度:O(1)
*/
class Solution {
public int trap(int[] height) {
int ans = 0;
int n = height.length;
for (int i = 1; i < n - 1; i++) {
int left_max = 0, right_max = 0;
for (int l = i - 1; l >= 0; l--) {
left_max = Math.max(left_max, height[l]);
}
for (int r = i + 1; r < n; r++) {
right_max = Math.max(right_max, height[r]);
}
ans += (Math.max(Math.min(left_max, right_max) - height[i], 0));
}
return ans;
}
}
|
1
2
|
执行用时:263 ms, 在所有 Java 提交中击败了5.05%的用户
内存消耗:38.1 MB, 在所有 Java 提交中击败了65.83%的用户
|
Solution2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
/*
空间换时间
预先存好每个元素i的左边最大和右边最大,分别用left_max[i]和right_max[i]来记录,最后要求的时候直接用存好的值
时间复杂度:O(n)
空间复杂度:O(n)
*/
class Solution {
public int trap(int[] height) {
int ans = 0;
int n = height.length;
int[] left_max = new int[n], right_max = new int[n];
// update left max value
for (int i = 1; i < n; i++) {
left_max[i] = Math.max(left_max[i - 1], height[i - 1]);
}
// update right max value
for (int i = n - 2; i >= 0; i--) {
right_max[i] = Math.max(right_max[i + 1], height[i + 1]);
}
for (int i = 1; i < n - 1; i++) {
ans += (Math.max(Math.min(left_max[i], right_max[i]) - height[i], 0));
}
return ans;
}
}
|
1
2
|
执行用时:1 ms, 在所有 Java 提交中击败了82.68%的用户
内存消耗:38.1 MB, 在所有 Java 提交中击败了63.43%的用户
|
Solution3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/*
因为对于每个元素我们要找到它的左边最大和右边最大然后取这两个值得较小值,然后减去当前高度得到存水容量
因此每次我们不关心两个值分别是多少,我们实际上只关心两个值较小的那个是多少
我们用left_max记录当前left元素左边的最大值,right_max记录当前right元素右边的最大值
当left_max < right_max时,此时对于left而言,left左侧的最大值已经得到,现在要看left右侧的最大值
如果在右边有比right_max小的元素,那么此时left右边最大的至少还是right_max > left_max;
如果在右边有比right_max大的元素xxx,那么就是说left_max < right_max < xxx
此时left两边的最大值的较小值就是left_max;
同理可以得到right两边的最大值的较小值就是right_max
时间复杂度:O(n)
空间复杂度:O(1)
*/
class Solution {
public int trap(int[] height) {
int ans = 0;
int n = height.length;
// left_max记录当前left元素左边的最大值,right_max记录当前right元素右边的最大值
// left_max: 0, 1, 2的左边最大值
// right_max: n-1, n-2, n-3的右边最大值
int left_max = 0, right_max = 0;
int left = 0, right = n - 1;
while (left < right) {
left_max = Math.max(left_max, height[left]); // 更新当前left左边最大值
right_max = Math.max(right_max, height[right]); // 更新当前right右边最大值
if (left_max < right_max) {
// 由于left_max < right_max,所以两个挡板中left_max必然是较低的
ans += left_max - height[left];
left++;
} else {
ans += right_max - height[right];
right--;
}
}
return ans;
}
}
|
1
2
|
执行用时:0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗:37.9 MB, 在所有 Java 提交中击败了90.72%的用户
|
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn )。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public double myPow(double x, int n) {
if (n == 1) return x;
if (n == 0) return 1;
if (n == -1) return 1 / x;
double half = myPow(x, n / 2);
double mod = myPow(x, n % 2);
return half * half * mod;
}
}
class Solution {
public double myPow(double x, int n) {
if (n == 0) return 1.0;
long b = n;
if (b < 0) {
x = 1 / x;
b = -b;
}
double res = 1.0;
while (b > 0) {
if ((b & 1) != 0) res *= x;
x *= x;
b /= 2;
}
return res;
}
}
|
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
/*
先根据第一个元素其次第二个元素升序排序
维护一个不重叠区间[start, end]
对于当前的i,如果能加入上一个不重叠区间,则更新不重叠区间的两端,也就是更新end
对于当前的i,如果不能加入上一个不重叠区间,则把上一个区间加入结果集,并更新当前区间[start, end]
对于最后一个单独的不重叠区间,要在遍历完之后单独加入结果集
*/
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new ArrayList<>();
Arrays.sort(intervals, (o1, o2) -> (o1[0] == o2[0]) ? o1[1] - o2[1] : o1[0] - o2[0]);
int start = intervals[0][0], end = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] <= end) {
end = Math.max(end, intervals[i][1]);
} else {
// 对于当前的i,如果不能加入上一个不重叠区间,则把上一个区间加入结果集,并更新当前区间
res.add(new int[]{start, end});
start = intervals[i][0];
end = intervals[i][1];
}
}
res.add(new int[]{start, end});
return res.toArray(new int[0][0]);
}
}
|
给你一个 无重叠的 *,*按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> res = new ArrayList<>();
int i = 0;
// [] [] [] [----] 原始区间的右端点一直在当前区间左端点左边,不用怀疑,直接丢进去
while (i < intervals.length && intervals[i][1] < newInterval[0]) {
res.add(intervals[i]);
i++;
}
// 一直合并到最后一个左端点大于end
while (i < intervals.length && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
res.add(newInterval);
// [----] [] [] [] 原始区间的左端点一直在当前区间的右端点右边,不用怀疑,直接丢进去
while (i < intervals.length) {
res.add(intervals[i]);
i++;
}
return res.toArray(new int[0][]);
}
}
|
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 '/' 开头),请你将其转化为更加简洁的规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,'//')都被视为单个斜杠 '/' 。 对于此问题,任何其他格式的点(例如,'...')均被视为文件/目录名称。
请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠
'/' 开头。
- 两个目录名之间必须只有一个斜杠
'/' 。
- 最后一个目录名(如果存在)不能 以
'/' 结尾。
- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含
'.' 或 '..')。
返回简化后得到的 规范路径 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public String simplifyPath(String path) {
// split完之后会出现四种元素
// 1. 空 2. "." 3. ".." 4. abc
Deque<String> doubleQueue = new LinkedList<>(); // 注意双向链表
String[] strs = path.split("/");
for (String str : strs) {
if ("".equals(str) || ".".equals(str)) continue; // 空 和 . 直接跳过
if ("..".equals(str)) {
if (!doubleQueue.isEmpty()) doubleQueue.pollLast();
} else {
doubleQueue.offerLast(str);
}
}
StringBuilder res = new StringBuilder();
if (doubleQueue.isEmpty()) {
res.append("/");
} else {
while (!doubleQueue.isEmpty()) {
res.append("/");
res.append(doubleQueue.pollFirst());
}
}
return res.toString();
}
}
|
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
// 两次遍历,第一次把0排好,第二次把1排好
public void sortColors(int[] nums) {
// ptr先全部指向0,然后指向1
// 第一轮先判断是否是0,是的话放到ptr上
// 第二轮判断是否是1,是的话放到prt上
int ptr = 0, n = nums.length, i = 0;
while (i < n) {
if (nums[i] == 0) {
swap(nums, i, ptr++);
}
i++;
}
i = ptr;
while (i < n) {
if (nums[i] == 1) {
swap(nums, i, ptr++);
}
i++;
}
}
// 一次遍历,设置两个指针,left存0,right存2
public void sortColors_1(int[] nums) {
int len = nums.length;
// i用来遍历,left存0,right存2
int i = 0, left = 0, right = len - 1;
while (i < len) {
if (nums[i] == 0 && i > left) {
swap(nums, i, left++);
} else if (nums[i] == 2 && i < right) {
swap(nums, i, right--);
} else {
i++;
}
}
}
private void swap(int[] nums, int a, int b) {
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
|
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
boolean flag = false;
public boolean exist(char[][] board, String word) {
if (board == null || board.length == 0) return false;
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
boolean[][] vis = new boolean[m][n];
dfs(word, 0, board, i, j, vis);
if (flag) return true;
}
}
return false;
}
private void dfs(String word, int index, char[][] board, int i, int j, boolean[][] vis) {
if (index == word.length()) {
flag = true;
return;
}
if ((i < 0 || i >= board.length) || (j < 0 || j >= board[0].length) || vis[i][j] || word.charAt(index) != board[i][j]) {
return;
}
vis[i][j] = true;
dfs(word, index + 1, board, i + 1, j, vis);
dfs(word, index + 1, board, i, j + 1, vis);
dfs(word, index + 1, board, i - 1, j, vis);
dfs(word, index + 1, board, i, j - 1, vis);
vis[i][j] = false;
}
}
|
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
暴力法,每次查看以当前高度所能产生的最宽的矩形,即分别向左向右找第一个小于当前元素的下标l,r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public int largestRectangleArea(int[] heights) {
// for each column, find the first column lower than it on its two sides
// left i right
// heights[i] * ((right - 1) - (left + 1) + 1);
int n = heights.length, res = 0;
for (int i = 0; i < n; i++) {
int left = i, right = i;
while (left >= 0 && heights[left] >= heights[i]) {
left--;
}
while (right < n && heights[right] >= heights[i]) {
right++;
}
res = Math.max(res, heights[i] * ((right - 1) - (left + 1) + 1));
}
return res;
}
}
|
对于向左向右找第一个小于当前元素的下标l,r,可以用单调递增栈来优化寻找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
单调栈
单调栈分为单调递增栈和单调递减栈
11. 单调递增栈即栈内元素保持单调递增的栈
12. 同理单调递减栈即栈内元素保持单调递减的栈
操作规则(下面都以单调递增栈为例)
21. 如果新的元素比栈顶元素大,就入栈
22. 如果新的元素较小,那就一直把栈内元素弹出来,直到栈顶比新元素小
加入这样一个规则之后,会有什么效果
31. 栈内的元素是递增的
32. 当元素出栈时,说明这个新元素是出栈元素向后找第一个比其小的元素
新的栈顶元素 < 出栈元素 < 当前元素
举个例子,配合下图,现在索引在 6 ,栈里是 1 5 6 。
接下来新元素是 2 ,那么 6 需要出栈。
当 6 出栈时,右边 2 代表是 6 右边第一个比 6 小的元素。
当元素出栈后,说明新栈顶元素是出栈元素向前找第一个比其小的元素
当 6 出栈时,5 成为新的栈顶,那么 5 就是 6 左边第一个比 6 小的元素。
作者:ikaruga
链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/84-by-ikaruga/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
|
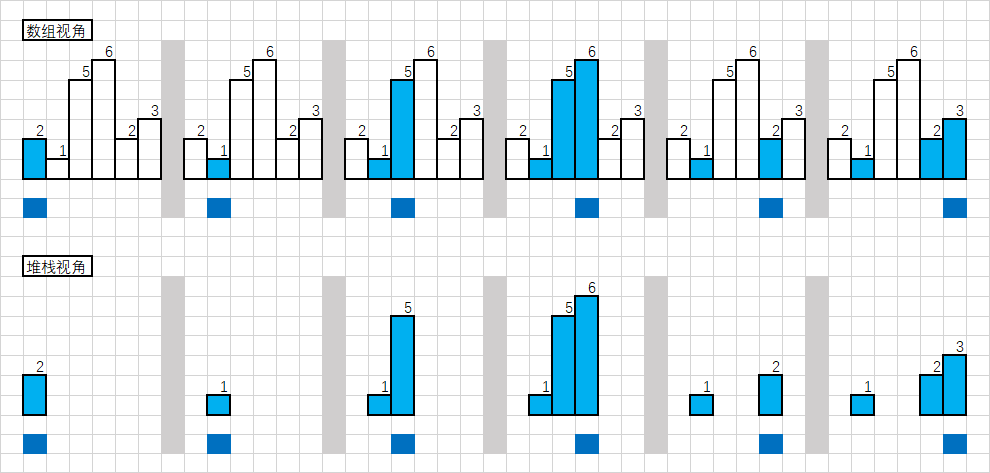
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int largestRectangleArea(int[] heights) {
int res = 0;
Deque<Integer> stack = new ArrayDeque<>();
int[] new_heights = new int[heights.length + 2];
System.arraycopy(heights, 0, new_heights, 1, heights.length);
for (int i = 0; i < new_heights.length; i++) {
while (!stack.isEmpty() && new_heights[stack.peek()] > new_heights[i]) {
int cur = stack.pop();
int l = stack.peek();
int r = i;
// l是cur左边第一个比他小的,r是cur右边第一个比他小的
// (r - 1) - (l + 1) + 1 = r - l - 1
res = Math.max(res, (r - l - 1) * new_heights[cur]);
}
stack.push(i);
}
return res;
}
}
|
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
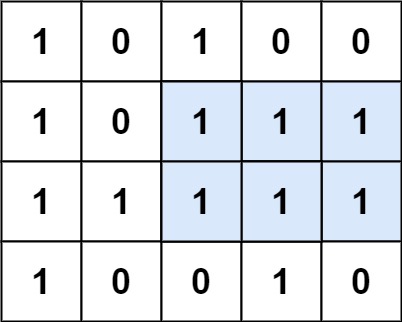
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
/*
每次将其看作是一串柱形,然后判断一串柱形所能形成的而最大面积
*/
class Solution {
public int maximalRectangle(char[][] matrix) {
if (matrix == null || matrix.length == 0) return 0;
int res = 0;
int m = matrix.length, n = matrix[0].length;
int[] heights = new int[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
heights[j] += 1;
} else {
heights[j] = 0;
}
}
res = Math.max(res, largestRectangleArea(heights));
}
return res;
}
private int largestRectangleArea(int[] heights) {
int[] new_heights = new int[heights.length + 2];
int res = 0;
System.arraycopy(heights, 0, new_heights, 1, heights.length);
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < new_heights.length; i++) {
while (!stack.isEmpty() && new_heights[stack.peek()] > new_heights[i]) {
int cur = stack.pop();
int l = stack.peek();
int r = i;
res = Math.max(res, new_heights[cur] * ((r - 1) - (l + 1) + 1));
}
stack.push(i);
}
return res;
}
}
|
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
// 自顶向下 dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j])
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
// dp[i][j]表示走到[i, j]处的最小路径和
// 对于最后一行判断最小的路径和
int m = triangle.size();
int[][] dp = new int[m][m];
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
dp[i][i] = dp[i - 1][i - 1] + triangle.get(i).get(i);
}
for (int i = 2; i < m; i++) {
for (int j = 1; j <= i - 1; j++) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
}
}
int res = Integer.MAX_VALUE;
for (int j = 0; j < m; j++) {
res = Math.min(res, dp[m - 1][j]);
}
return res;
}
}
// 自底向上 dp[i][j] <- min(dp[i + 1][j + 1], dp[i + 1][j])
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int m = triangle.size();
int[][] dp = new int[m + 1][m + 1];
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < triangle.get(i).size(); j++) {
dp[i][j] = triangle.get(i).get(j) + Math.min(dp[i + 1][j + 1], dp[i + 1][j]);
}
}
return dp[0][0];
}
}
// 自底向上 空间优化
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int m = triangle.size();
int[] dp = new int[m + 1];
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < triangle.get(i).size(); j++) {
dp[j] = triangle.get(i).get(j) + Math.min(dp[j + 1], dp[j]);
}
}
return dp[0];
}
}
// 还可以原地修改,因为用完当前层就不用了,所以可以原地修改数组
|
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
// 不要两边遍历,对于每个数字只让他往右边遍历,这样的话对于 1 2 3,遍历完 1 2 3之后,到了2,就不用重新得到1 2 3一次了
class Solution {
public int longestConsecutive(int[] nums) {
if (nums == null || nums.length == 0) return 0;
Set<Integer> set = new HashSet<>();
for (int num : nums) {
set.add(num);
}
int res = 1;
for (int num : nums) {
if (!set.contains(num - 1)) {
int len = 1;
while (set.contains(++num)) {
len++;
}
res = Math.max(res, len);
}
}
return res;
}
}
|
给你一个字符串 s 和一个字符串列表 wordDict 作为字典,判定 s 是否可以由空格拆分为一个或多个在字典中出现的单词。
**说明:**拆分时可以重复使用字典中的单词。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
int n = s.length();
boolean[] dp = new boolean[n + 1];
/*
dp[i] 表示 [0, i-1] 中的元素是否可以拆分到 wordDict 中
dp[j] 表示 [0, j - 1], 则要求 dp[j] && [j, i - 1]可以找到
*/
dp[0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDict.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[n];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
class Solution {
public String reverseWords(String s) {
String temp = cleanExtraSpace(s);
char[] chars = temp.toCharArray();
reverse(chars, 0, chars.length - 1);
reverseWord(chars);
return new String(chars);
}
private String cleanExtraSpace(String s) {
char[] chars = s.toCharArray();
// 移除多余的空格
int left = 0, right = chars.length - 1;
StringBuilder sb = new StringBuilder();
while (chars[left] == ' ') left++;
while (chars[right] == ' ') right--; // 先去除两端多余的空格
while (left <= right) {
if (chars[left] == ' ') {
sb.append(chars[left]); // 遇到中间的空格只加入一次
while (left <= right && chars[left] == ' ') {
left++;
}
} else {
sb.append(chars[left]);
left++;
}
}
return sb.toString();
}
private void reverse(char[] chars, int left, int right) {
while (left < right) {
char temp = chars[left];
chars[left] = chars[right];
chars[right] = temp;
left++;
right--;
}
}
private void reverseWord(char[] chars) {
int left = 0, right = 0, n = chars.length;
while (right < n) {
while (left < n && chars[left] == ' ') {
left++;
}
right = left;
while (right < n && chars[right] != ' ') {
right++;
}
reverse(chars, left, right - 1);
left = right;
}
}
}
|
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 '.' 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
- 如果
*version1* > *version2* 返回 1,
- 如果
*version1* < *version2* 返回 -1,
- 除此之外返回
0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public int compareVersion(String version1, String version2) {
int i = 0, j = 0;
while (i < version1.length() || j < version2.length()) {
int a = 0, b = 0;
while (i < version1.length() && version1.charAt(i) != '.') {
a = a * 10 + (version1.charAt(i++) - '0');
}
while (j < version2.length() && version2.charAt(j) != '.') {
b = b * 10 + (version2.charAt(j++) - '0');
}
if (a > b) return 1;
else if (a < b) return -1;
i++;
j++;
}
return 0;
}
}
|
难度中等718
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int[] twoSum(int[] numbers, int target) {
int[] res = new int[2];
if (numbers == null || numbers.length == 0) return res;
int left = 0, right = numbers.length - 1;
while (left < right) {
int sum = numbers[left] + numbers[right];
if (sum == target) {
return new int[]{left + 1, right + 1};
} else if (sum < target) {
while (left < right && numbers[left] == numbers[left + 1]) left++;
left++;
} else {
while (left < right && numbers[right] == numbers[right - 1]) right--;
right--;
}
}
return res;
}
}
|
难度中等634
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
// 层序遍历,获取每一层的最后一个结点
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Deque<TreeNode> queue = new LinkedList<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
if (i == size - 1) res.add(queue.peek().val);
p = queue.poll();
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
}
return res;
}
}
|
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
- 快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums, 0, nums.length - 1, k - 1);
}
private int quickSelect(int[] nums, int left, int right, int index) {
int mid = partition(nums, left, right);
if (mid == index) {
return nums[mid];
} else if (mid < index) {
return quickSelect(nums, mid + 1, right, index);
} else {
return quickSelect(nums, left, mid - 1, index);
}
}
private int partition(int[] nums, int left, int right) {
/*
为了防止pivot最大导致快排效果裂开,将基准随机交换一个元素
每次让left元素跟后面随机一个元素交换,然后再置为pivot
*/
int random_index = (int) (left + Math.random() * (right - left + 1));
int temp = nums[left];
nums[left] = nums[random_index];
nums[random_index] = temp;
// 加了上面的交换之后速度 9ms -> 1ms
int pivot = nums[left];
while (left < right) {
// 从右到左找到第一个比基准大的
while (left < right && nums[right] <= pivot) {
right--;
}
// 放入left
nums[left] = nums[right];
// 从左到右找到第一个比基准小的
while (left < right && nums[left] >= pivot) {
left++;
}
// 放入right
nums[right] = nums[left];
}
// 放入基准
nums[left] = pivot;
return left;
}
}
|
- 优先队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
public class Solution {
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
// 使用一个含有 k 个元素的最小堆,PriorityQueue 底层是动态数组,为了防止数组扩容产生消耗,可以先指定数组的长度
PriorityQueue<Integer> minHeap = new PriorityQueue<>(k);
for (int i = 0; i < k; i++) {
minHeap.offer(nums[i]);
}
for (int i = k; i < len; i++) {
int topElement = minHeap.peek();
// 只要当前遍历的元素比堆顶元素大,堆顶弹出,遍历的元素进去
if (nums[i] > topElement) {
minHeap.poll();
minHeap.offer(nums[i]);
}
}
return minHeap.peek();
}
}
|
-
堆排序
顺序排序,建大根堆
求最大的k个/第k个结点,建小根堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
/*
手动设置一个大小为k的小根堆,最后小根堆的根节点就是第k个最大的节点
*/
class Solution {
public int findKthLargest(int[] nums, int k) {
//前K个元素原地建堆
buildHeap(nums,k);
//遍历余下的元素
for(int i = k; i < nums.length; i++){
//比堆顶小,就跳过
if(nums[i] < nums[0]) continue;
//比堆顶大,与堆顶元素交换后重新堆化
swap(nums,i,0);
heapify(nums,k,0);
}
//K个元素的小堆顶的堆顶就是第K大元素
return nums[0];
}
/**
建堆函数
从最后一个非叶子节点开始堆化,其下标为节点数n/2 - 1
*/
private void buildHeap(int[] nums,int len){
for(int i = len/2 - 1; i >= 0; i--){
heapify(nums,len,i);
}
}
/**
堆化函数。建立小顶堆
父节点的下标为i,左右孩子的下标分别为2i+1 和 2i+2
*/
private void heapify(int[] nums,int len, int i){
while(true){
//临时变量minPos用于存储最小值的下标。先假设父节点最小
int minPos = i;
//和左节点比较
if(2 * i + 1 < len && nums[2 * i + 1] < nums[i]){
minPos = 2 * i + 1;
}
//和右节点比较
if(2 * i + 2 < len && nums[2 * i + 2] < nums[minPos]){
minPos = 2 * i + 2;
}
//如果minpos没有变化,说明父节点已经是最小了,直接跳出
if(minPos == i) break;
//否则交换节点
swap(nums,i,minPos);
//交换后可能会引起下面大小关系变化,更新父节点,继续堆化
i = minPos;
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
|
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。int pop() 移除并返回栈顶元素。int top() 返回栈顶元素。boolean empty() 如果栈是空的,返回 true ;否则,返回 false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class MyStack {
Deque<Integer> inQueue;
Deque<Integer> outQueue;
public MyStack() {
inQueue = new LinkedList<>();
outQueue = new LinkedList<>();
}
public void push(int x) {
inQueue.offer(x);
}
public int pop() {
int size = inQueue.size();
for (int i = 0; i < size - 1; i++) {
outQueue.offer(inQueue.poll());
}
int res = inQueue.poll();
Deque<Integer> temp = inQueue;
inQueue = outQueue;
outQueue = temp;
return res;
}
public int top() {
int size = inQueue.size();
for (int i = 0; i < size - 1; i++) {
outQueue.offer(inQueue.poll());
}
int res = inQueue.peek();
Deque<Integer> temp = inQueue;
inQueue = outQueue;
outQueue = temp;
inQueue.offer(outQueue.poll());
return res;
}
public boolean empty() {
return inQueue.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
|
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头的元素boolean empty() 如果队列为空,返回 true ;否则,返回 fals
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
class MyQueue {
Deque<Integer> inStack;
Deque<Integer> outStack;
public MyQueue() {
inStack = new LinkedList<>();
outStack = new LinkedList<>();
}
public void push(int x) {
inStack.push(x);
}
public int pop() {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
int head = outStack.pop();
while (!outStack.isEmpty()) {
inStack.push(outStack.pop());
}
return head;
}
public int peek() {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
int head = outStack.peek();
while (!outStack.isEmpty()) {
inStack.push(outStack.pop());
}
return head;
}
public boolean empty() {
return inStack.isEmpty();
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/
|
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public int maximalSquare(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
int m = matrix.length, n = matrix[0].length;
int[][] dp = new int[m][n];
int max_len = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = 1 + Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]);
}
max_len = Math.max(max_len, dp[i][j]);
}
}
}
return max_len * max_len;
}
}
|
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
class Solution {
// Collections.sort
public int[] topKFrequent_1(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
List<Map.Entry<Integer, Integer>> list = new LinkedList<>(map.entrySet());
Collections.sort(list, (o1, o2) -> (o2.getValue() - o1.getValue()));
int[] res = new int[k];
for (int i = 0; i < k; i++) {
res[i] = list.get(i).getKey();
}
return res;
}
// priorityQueue
public int[] topKFrequent_2(int[] nums, int k) {
int[] res = new int[k];
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
// 根据entry的值构建大小为k的小顶堆,遍历完堆中的就是值最大的k个entry
Queue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((o1, o2) -> (o1.getValue() - o2.getValue()));
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
queue.offer(entry);
if (queue.size() > k) {
queue.poll();
}
}
int i = 0;
while (!queue.isEmpty()) {
res[i++] = queue.poll().getKey();
}
return res;
}
// 桶排序
public List<Integer> topKFrequent_3(int[] nums, int k) {
if (nums == null || nums.length == 0 || k == 0)
return new ArrayList<>();
LinkedList<Integer>[] fre = new LinkedList[nums.length + 1];
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
for (Integer key : map.keySet()) {
int value = map.get(key);
if (fre[value] == null) {
fre[value] = new LinkedList<>();
}
fre[value].add(key);
}
List<Integer> res = new ArrayList<>();
//倒序遍历频率数组,这样可以获取频率从高到低的数字
for (int i = fre.length - 1; i >= 0 && res.size() < k; i--) {
LinkedList<Integer> list = fre[i];
//如果当前频率没有数字,跳过
if (list == null) {
continue;
}
//相同频率的数字可能有多个,这个只取k个就行,注意顺序是从左往右取
while (res.size() < k && !list.isEmpty()) {
res.add(list.removeFirst());
}
}
return res;
}
}
|
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public int thirdMax(int[] nums) {
Integer first = null, second = null, third = null;
for (Integer cur : nums) {
if(cur.equals(first) || cur.equals(second) || cur.equals(third)) continue;
if(first == null || cur > first) {
third = second;
second = first;
first = cur;
} else if(second == null || cur > second) {
third = second;
second = cur;
} else if(third == null || cur > third) {
third = cur;
}
}
return third == null ? first : third;
}
}
|
给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Solution {
// 时间复杂度 O(n)
// 空间复杂度 O(n)
// 维护leftMul rightMul,然后对应相乘
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] left = new int[n];
int[] right = new int[n];
left[0] = 1;
for (int i = 1; i < n; i++) {
left[i] = left[i - 1] * nums[i - 1];
}
right[n - 1] = 1;
for (int j = n - 2; j >= 0; j--) {
right[j] = right[j + 1] * nums[j + 1];
}
int[] res = new int[n];
for (int i = 0; i < n; i++) {
res[i] = left[i] * right[i];
}
return res;
}
// 时间复杂度 O(n)
// 空间复杂度 O(1)
// 将left存在res中,遍历right的时候直接把相应的right乘以res中的值然后赋值给res
public int[] productExceptSelf_1(int[] nums) {
int n = nums.length;
int[] res = new int[n];
int left = 1;
for (int i = 0; i < n; i++) {
if (i > 0) {
left *= nums[i - 1];
}
res[i] = left;
}
int right = 1;
for (int j = n - 1; j >= 0; j--) {
if (j < n - 1) {
right *= nums[j + 1];
}
res[j] *= right;
}
return res;
}
}
|
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 最大的k个用小根堆,下标0处存的是最小的元素
// 那么这里要用大根堆,下标0处存的是最大的元素 -> 超时 49 / 61 个通过测试用例
int[] res = new int[nums.length - k + 1];
int idx = 0, removeIdx = 0;
PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> (nums[o2] - nums[o1]));
for (int i = 0; i < nums.length; i++) {
queue.offer(i);
if (queue.size() == k) {
res[idx++] = nums[queue.peek()];
queue.remove(removeIdx++);
}
}
return res;
}
}
// 可以用单调递减栈,栈中存放的是根据下标元素降序,每次新元素加入要判断是否要弹出较小的结点
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length < 2) return nums;
// 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数值按从大到小排序
Deque<Integer> queue = new LinkedList();
// 结果数组
int[] res = new int[nums.length - k + 1];
// 遍历nums数组
for (int i = 0; i < nums.length; i++) {
// 保证从大到小 如果前面数小则需要依次弹出,直至满足要求
while (!queue.isEmpty() && nums[queue.peekLast()] <= nums[i]) {
queue.pollLast();
}
// 添加当前值对应的数组下标
queue.offerLast(i);
// 判断当前队列中队首的最大值是否有效,即该元素是否还在窗口内
if (i - queue.peekFirst() + 1 > k) {
queue.pollFirst();
}
// 当窗口长度为k时 保存当前窗口中最大值
if (i >= k - 1) {
res[i + 1 - k] = nums[queue.peekFirst()];
}
}
return res;
}
}
|
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
- dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
/*
dp[i]表示表示数字i所需要的最少的完全平方数
*/
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1];
dp[0] = 0;
for (int i = 1; i < n + 1; i++) {
dp[i] = Integer.MAX_VALUE;
for (int j = 1; j * j <= i; j++) {
dp[i] = Math.min(dp[i], 1 + dp[i - j * j]);
}
}
return dp[n];
}
}
|
- 数学
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/*
任何数都可以表示为4个完全平方数的和,即答案为 1 / 2 / 3 / 4
1 <=> a^2 = num;
2 <=> a^2 + b^2 = num;
4 <=> 4a*(8b+7) = num;
3 <=> 剩余情况
*/
class Solution {
public int numSquares(int n) {
if (isSquare(n)) return 1;
if (checkAnswer4(n)) return 4;
// 判断 i^2 + j^2 = n
for (int i = 1; i * i <= n; i++) {
int j = n - i * i;
if (isSquare(j)) return 2;
}
return 3;
}
private boolean isSquare(int num) {
int x = (int) Math.sqrt(num);
return x * x == num;
}
// (4a)*(8b+7) == num 则是由四个平方数组成
private boolean checkAnswer4(int num) {
while (num % 4 == 0) {
num /= 4;
}
return num % 8 == 7;
}
}
|
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class MedianFinder {
Queue<Integer> maxQueue; // 最大堆,根节点值最大,用来存较小的一半值
Queue<Integer> minQueue; // 最小堆,根节点值最小,用来存较大的一半值
public MedianFinder() {
maxQueue = new PriorityQueue<>((o1, o2) -> (o2 - o1));
minQueue = new PriorityQueue<>((o1, o2) -> (o1 - o2));
}
// 大根堆 小根堆
// maxQueue minQueue
// size(maxQueue) = 1 + size(minQueue)
// 插入元素,先插入到maxQueue然后弹出一个元素插入到minQueuee
// 查找元素,就是 maxQueue的根节点
// size(minQueue) = size(maxQueue)
// 插入元素,先插入到minQuuee中然后弹出一个元素插入到maxQueue中
// 查找元素,当前两个根的平均
public void addNum(int num) {
if (maxQueue.size() == minQueue.size() + 1) {
maxQueue.offer(num);
minQueue.offer(maxQueue.poll());
} else {
minQueue.offer(num);
maxQueue.offer(minQueue.poll());
}
}
public double findMedian() {
if (maxQueue.size() == minQueue.size() + 1) {
return maxQueue.peek();
} else {
return (minQueue.peek() + maxQueue.peek()) / 2.0;
}
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
|
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class Solution {
List<String> res = new ArrayList<>();
public List<String> removeInvalidParentheses(String s) {
int lremove = 0, rremove = 0;
for (char c : s.toCharArray()) {
if (c == '(') {
lremove++;
} else {
if (lremove == 0) {
rremove++;
} else {
lremove--;
}
}
}
helper(s, 0, lremove, rremove);
return res;
}
private void helper(String str, int start, int lremove, int rremove) {
if (lremove == 0 && rremove == 0 && isValid(str)) {
res.add(str);
return;
}
for (int i = start; i < str.length(); i++) {
if (i != start && str.charAt(i) == str.charAt(i - 1)) {
continue;
}
// 如果剩余的字符无法满足去掉的数量要求,直接返回
if (lremove + rremove > str.length() - i) {
return;
}
// 尝试去掉一个左括号
if (lremove > 0 && str.charAt(i) == '(') {
helper(str.substring(0, i) + str.substring(i + 1), i, lremove - 1, rremove);
}
// 尝试去掉一个右括号
if (rremove > 0 && str.charAt(i) == ')') {
helper(str.substring(0, i) + str.substring(i + 1), i, lremove, rremove - 1);
}
}
}
private boolean isValid(String s) {
int cnt = 0;
char[] chars = s.toCharArray();
for (char c : chars) {
if (c == '(') {
cnt++;
} else if (c == ')') {
cnt--;
if (cnt < 0) return false;
}
}
return cnt == 0;
}
}
|
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public int[] countBits(int n) {
int[] res = new int[n + 1];
for (int i = 1; i <= n; i++) {
res[i] = res[i & (i - 1)] + 1;
}
return res;
}
public int[] countBits1(int n) {
int[] res = new int[n + 1];
for (int i = 1; i <= n; i++) {
res[i] = res[i >> 1] + (i & 1);
}
return res;
}
}
|
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
class Solution {
public String decodeString(String s) {
char[] charArray = s.toCharArray();
Deque<Character> stack = new LinkedList<>();
for (char c : charArray) {
if (c != ']') {
stack.push(c);
} else {
StringBuilder subStr = new StringBuilder(); // 存储数字 * []中的字符串
// 得到字符串从栈中弹出之后进行头插得到正序的子字符串
while (!stack.isEmpty() && (stack.peek() >= 'a' && stack.peek() <= 'z')) {
subStr.insert(0, stack.pop());
}
// 弹出 '['
stack.pop();
// 得到从栈中弹出之后进行运算得到的次数
int exp = 0, cnt = 0;
while (!stack.isEmpty() && (stack.peek() >= '0' && stack.peek() <= '9')) {
cnt = (int) ((stack.pop() - '0') * Math.pow(10, exp++)) + cnt;
}
// 将 cnt[subStr]格式的进行转换插入到栈中
while (cnt > 0) {
for (char ch : subStr.toString().toCharArray()) {
stack.push(ch);
}
cnt--;
}
}
}
// 由于栈是从栈顶遍历到栈底的,因此要进行逆转操作,此处使用头插法
StringBuilder res = new StringBuilder();
for (char c : stack) {
res.insert(0, c);
}
return res.toString();
}
}
class Solution {
public String decodeString(String s) {
char[] charArr = s.toCharArray();
Deque<StringBuilder> sbStack = new LinkedList<>();
Deque<Integer> multiStack = new LinkedList<>();
StringBuilder curStr = new StringBuilder();
int multi = 0;
for (char ch : charArr) {
if (ch >= '0' && ch <= '9') {
multi = multi * 10 + (ch - '0');
} else if (ch == '[') {
multiStack.push(multi);
sbStack.push(curStr);
multi = 0;
curStr = new StringBuilder();
} else if (ch == ']') {
StringBuilder lastSb = sbStack.pop();
int times = multiStack.pop();
for (int i = 0; i < times; i++) {
lastSb.append(curStr);
}
curStr = lastSb;
} else {
curStr.append(ch);
}
}
return curStr.toString();
}
}
|
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
class Solution {
// 每次新建固定大小的窗口
public List<Integer> findAnagrams_1(String s, String p) {
List<Integer> res = new ArrayList<>();
int[] pMap = new int[26];
for (char c : p.toCharArray()) {
pMap[c - 'a'] += 1;
}
for (int i = 0; i <= s.length() - p.length(); i++) {
int[] subMap = new int[26];
String sub = s.substring(i, i + p.length());
for (char c : sub.toCharArray()) {
subMap[c - 'a'] += 1;
}
if (Arrays.equals(pMap, subMap)) res.add(i);
}
return res;
}
// 优化1:这个窗口每次都是向后移动一位,所以除了第一位和最后一位,中间的都是不变的
public List<Integer> findAnagrams_2(String s, String p) {
List<Integer> res = new ArrayList<>();
if (s.length() < p.length()) return res;
int[] pMap = new int[26], subMap = new int[26];
for (char c : p.toCharArray()) {
pMap[c - 'a'] += 1;
}
for (int i = 0; i < p.length(); i++) {
subMap[s.charAt(i) - 'a'] += 1;
}
if (Arrays.equals(pMap, subMap)) res.add(0);
// 窗口的起始坐标范围为 [0, s.length() - p.length()],所以判断是否可以向后滑动要求最后一个起始坐标不是最后一个
for (int i = 0; i <= s.length() - p.length() - 1; i++) {
// 此时可以向后移动, 区间范围为 [i, i + p.length() - 1]
subMap[s.charAt(i) - 'a']--;
subMap[s.charAt(i + p.length()) - 'a']++;
if (Arrays.equals(pMap, subMap)) res.add(i + 1);
}
return res;
}
// 上面优化1开了两个数组,其实可以只开一个数组,当遍历完窗口时,将对应的值减少,如果最后都是1,说明其实就是对应相等
public List<Integer> findAnagrams(String s, String p) {
int sLen = s.length(), pLen = p.length();
if (sLen < pLen) {
return new ArrayList<Integer>();
}
List<Integer> ans = new ArrayList<Integer>();
// count表示当前窗口哪些字母多了或者少了
int[] count = new int[26];
for (int i = 0; i < pLen; ++i) {
count[s.charAt(i) - 'a']++;
count[p.charAt(i) - 'a']--;
}
int differ = 0;
for (int val : count) {
if (val != 0) differ++;
}
if (differ == 0) ans.add(0);
for (int i = 0; i <= sLen - pLen - 1; ++i) {
int old_head = count[s.charAt(i) - 'a'];
if (old_head == 1) { // 窗口中字母 s[i] 的数量与字符串 p 中的数量从不同变得相同
differ--;
} else if (old_head == 0) { // 窗口中字母 s[i] 的数量与字符串 p 中的数量从相同变得不同
differ++;
}
count[s.charAt(i) - 'a']--;
int new_tail = count[s.charAt(i + pLen) - 'a'];
if (new_tail == -1) { // 窗口中字母 s[i+pLen] 的数量与字符串 p 中的数量从不同变得相同
differ--;
} else if (new_tail == 0) { // 窗口中字母 s[i+pLen] 的数量与字符串 p 中的数量从相同变得不同
differ++;
}
count[s.charAt(i + pLen) - 'a']++;
if (differ == 0) ans.add(i + 1);
}
return ans;
}
}
|
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public List<Integer> findDisappearedNumbers_1(int[] nums) {
List<Integer> res = new ArrayList<>();
Map<Integer, Integer> map = new HashMap<>();
int n = nums.length;
for (int num = 1; num <= n; num++) {
map.put(num, 1);
}
for (int num : nums) {
map.put(num, 0);
}
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
if (entry.getValue() != 0) {
res.add(entry.getKey());
}
}
return res;
}
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (nums[Math.abs(nums[i]) - 1] > 0) {
nums[Math.abs(nums[i]) - 1] = -nums[Math.abs(nums[i]) - 1];
}
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
res.add(i + 1);
}
}
return res;
}
}
|
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
// 1. 暴力,每次固定一个开始数字然后往右遍历
// 2. 前缀和
class Solution {
// 用prefix[i]表示前i个元素的和
public int subarraySum_1(int[] nums, int k) {
int len = nums.length;
int[] prefix = new int[len + 1];
prefix[0] = 0;
for (int i = 0; i < len; i++) {
prefix[i + 1] = prefix[i] + nums[i];
}
int cnt = 0;
for (int i = 0; i < len; i++) {
for (int j = i; j < len; j++) {
if (prefix[j + 1] - prefix[i] == k) cnt++;
}
}
return cnt;
}
// 用prefix的map来记录前缀和对应其出现的次数
// map记录前缀和可以用的种数
public int subarraySum(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
int sum = 0, res = 0;
map.put(0, 1);
for(int num : nums) {
sum += num;
if (map.containsKey(sum - k)) {
res += map.get(sum - k);
}
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return res;
}
}
|
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
// 1. 检查第i位时,将n与2^i次方进行与运算,如果与完之后等于2^i,说明该位置是1,如果与完之后等于0,说明该位置是0
// 1 0 0 1 0
// 0 0 0 1 0
public int hammingWeight(int n) {
int cnt = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) cnt++;
}
return cnt;
}
// 2. 每次检查最低位是不是1,是则计数,每次判断完最低位之后都要右移一位
public int hammingWeight_1(int n) {
int cnt = 0;
for (int i = 0; i < 32; i++) {
if ((n & 1) == 1) cnt++;
n = n >> 1;
}
return cnt;
}
// 3. 通过n & (n-1)来将n最低位的1置为0,直到n等于0为止
// n: 1 1 0 1 | 1 0 0 0
// n-1: 1 1 0 1 | 0 1 1 1
// n & (n-1): 1 1 0 1 | 0 0 0 0
public int hammingWeight_2(int n) {
int cnt = 0;
while (n != 0) {
n = n & (n - 1);
cnt++;
}
return cnt;
}
}
|
难度中等757
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
// dfs
class Solution {
public int findCircleNum(int[][] isConnected) {
// 从一个没有标记过的元素开始dfs,dfs的元素标记为已访问
// dfs结束将结果加1
int res = 0;
int n = isConnected.length;
boolean[] vis = new boolean[n];
for (int i = 0; i < n; i++) {
if (!vis[i]) {
dfs(isConnected, i, vis);
res++;
}
}
return res;
}
private void dfs(int[][] isConnected, int i, boolean[] vis) {
vis[i] = true;
for (int j = 0; j < isConnected.length; j++) {
if (isConnected[i][j] == 1 && !vis[j]) {
dfs(isConnected, j, vis);
}
}
}
}
// bfs
class Solution {
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
boolean[] vis = new boolean[n];
Deque<Integer> queue = new LinkedList<>();
int res = 0;
for (int i = 0; i < n; i++) {
if (!vis[i]) {
res++;
queue.offer(i);
vis[i] = true;
while (!queue.isEmpty()) {
int v = queue.poll();
for (int w = 0; w < n; w++) {
if (isConnected[v][w] == 1 && !vis[w]) {
queue.offer(w);
vis[w] = true;
}
}
}
}
}
return res;
}
}
|
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public TreeNode convertBST(TreeNode root) {
TreeNode p = root;
Deque<TreeNode> stack = new LinkedList<>();
int largerSum = 0;
while (!stack.isEmpty() || p != null) {
while (p != null) {
stack.push(p);
p = p.right;
}
p = stack.pop();
p.val = p.val + largerSum;
largerSum = p.val;
p = p.left;
}
return root;
}
}
|
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public String addStrings(String num1, String num2) {
StringBuilder res = new StringBuilder();
int i = num1.length() - 1, j = num2.length() - 1, carry = 0;
while(i >= 0 || j >= 0){
int n1 = i >= 0 ? num1.charAt(i) - '0' : 0;
int n2 = j >= 0 ? num2.charAt(j) - '0' : 0;
int tmp = n1 + n2 + carry;
carry = tmp / 10;
res.append(tmp % 10);
i--;
j--;
}
if(carry == 1) res.append(1);
return res.reverse().toString();
}
}
|
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
**注意:**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
class Solution {
public String multiply(String num1, String num2) {
if (num1 == null || num2 == null || "0".equals(num1) || "0".equals(num2) || num1.length() == 0 || num2.length() == 0) return "0";
String ans = "0";
for (int i = num2.length() - 1; i >= 0; i--) {
int y = num2.charAt(i) - '0';
StringBuilder sb = new StringBuilder();
for (int j = num2.length() - 1; j > i; j--) {
sb.append("0");
}
int carry = 0;
for (int j = num1.length() - 1; j >= 0; j--) {
int x = num1.charAt(j) - '0';
int mul = x * y + carry;
int cur = mul % 10;
carry = mul / 10;
sb.append(cur);
}
if (carry != 0) sb.append(carry);
ans = add(ans, sb.reverse().toString());
}
return ans;
}
private String add(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1, carry = 0;
StringBuilder sb = new StringBuilder();
while (i >= 0 || j >= 0 || carry != 0) {
int n1 = i >= 0 ? num1.charAt(i) - '0': 0;
int n2 = j >= 0 ? num2.charAt(j) - '0' : 0;
int sum = n1 + n2 + carry;
carry = sum / 10;
sb.append(sum % 10);
i--;
j--;
}
return sb.reverse().toString();
}
}
class Solution {
public String multiply(String num1, String num2) {
if (num1 == null || num2 == null || "0".equals(num1) || "0".equals(num2) || num1.length() == 0 || num2.length() == 0) return "0";
// m n 结果最长为 m + n
// num1[m] * num2[n] 的结果存放在 num1[i] x num2[j] 的结果为 tmp(位数为两位,"0x","xy"的形式),其第一位位于 res[i+j],第二位位于 res[i+j+1]。
int m = num1.length(), n = num2.length();
int[] helper = new int[m + n];
int carry = 0;
for (int i = m - 1; i >= 0; i--) {
int x = num1.charAt(i) - '0';
for (int j = n - 1; j >= 0; j--) {
int y = num2.charAt(j) - '0';
int sum = (helper[i + j + 1] + x * y);
helper[i + j + 1] = sum % 10;
helper[i + j] += sum / 10; // 进到上一位可能有很多种可能进上去
}
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < helper.length; i++) {
if (i == 0 && helper[i] == 0) continue;
sb.append(helper[i]);
}
return sb.toString();
}
}
|
难度中等338
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int maxSubarraySumCircular(int[] nums) {
// maxDp/minDp表示以i结尾的子数组的最大/最小和
// 注意要是全为负数,则返回max
int n = nums.length;
int[] maxDp = new int[n], minDp = new int[n];
maxDp[0] = nums[0];
minDp[0] = nums[0];
int max = maxDp[0], min = maxDp[0], sum = nums[0];
for (int i = 1; i < n; i++) {
maxDp[i] = Math.max(maxDp[i - 1] + nums[i], nums[i]);
max = Math.max(max, maxDp[i]);
minDp[i] = Math.min(minDp[i - 1] + nums[i], nums[i]);
min = Math.min(min, minDp[i]);
sum += nums[i];
}
if (max < 0) return max;
return Math.max(max, sum - min);
}
}
|
请你编写一个程序来计算两个日期之间隔了多少天。
日期以字符串形式给出,格式为 YYYY-MM-DD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
int[] m_days = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
public int daysBetweenDates(String date1, String date2) {
String[] strs1 = date1.split("-");
String[] strs2 = date2.split("-");
int year1 = Integer.parseInt(strs1[0]), month1 = Integer.parseInt(strs1[1]), day1 = Integer.parseInt(strs1[2]);
int year2 = Integer.parseInt(strs2[0]), month2 = Integer.parseInt(strs2[1]), day2 = Integer.parseInt(strs2[2]);
return Math.abs(getGap(year2, month2, day2) - getGap(year1, month1, day1));
}
private int getGap(int year, int month, int day) {
int gap = 0;
for (int y = 1971; y < year; y++) {
gap += isSpecialYear(y) ? 366 : 365;
}
for (int i = 1; i < month; i++) {
if (i == 2) gap += (28 + (isSpecialYear(year) ? 1 : 0));
else gap += m_days[i];
}
return gap + day;
}
private boolean isSpecialYear(int year) {
return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0);
}
}
|
给你一个字符串 s 。请返回 s 中最长的 超赞子字符串 的长度。
「超赞子字符串」需满足满足下述两个条件:
- 该字符串是
s 的一个非空子字符串
- 进行任意次数的字符交换后,该字符串可以变成一个回文字符串
首先,超赞字符串 <=> 字符串中最多只有一个字符的总个数为奇数
我们不需要知道具体出现多少个,可以用1来表示出现了奇数次,用0来表示出现了偶数次
那么对于这个字符串可以将其表示为 status = 00 0000 0010这样
其中1表示该位的数字出现了奇数次,区间为 [i, j] = [0, j] - [0, i-1]
[0, j] 和 [0, i-1] 的状态要么一样,要么只有一位不一样
一样的话,直接获取该状态的下标,两者相减,否则将当前状态加入
不一样的话,对status的每一位先反转即1->0, 0->1,然后找反转后status是否存在过,存在过也可以更新
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public int longestAwesome(String s) {
// 记录 status 与其对应的下标
// status 就是记录每个出现的次数是偶数还是奇数
// 每次加入新的字符,将它参与status计算,判断之前是否出现相同的status
// 或者只有一位不一样的status
// 有的话都要参与结果判断
int res = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, -1);
int status = 0;
for (int i = 0; i < s.length(); i++) {
int num = s.charAt(i) - '0';
status ^= (1 << num);
if (map.containsKey(status)) {
res = Math.max(res, i - map.get(status));
} else {
map.put(status, i);
}
for (int j = 0; j <= 9; j++) {
if (map.containsKey(status ^ (1 << j))) {
res = Math.max(res, i - map.get(status ^ (1 << j)));
}
}
}
return res;
}
}
|
难度简单75
给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
请你找到这个数组里第 k 个缺失的正整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public int findKthPositive(int[] arr, int k) {
int n = arr.length, begin = 1, cnt;
for (int num : arr) {
if (begin < num) {
// [begin, num)
cnt = num - 1 - begin + 1 <= k ? num - begin : k;
k -= cnt;
if (k == 0) return begin + cnt - 1;
}
begin = num + 1;
}
return arr[n - 1] + k;
}
}
|
难度中等25
给你一个整数数组 nums 和一个整数 k 。请你向 nums 中追加 k 个 未 出现在 nums 中的、互不相同 的 正 整数,并使结果数组的元素和 最小 。
返回追加到 nums 中的 k 个整数之和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public long minimalKSum(int[] nums, int k) {
// 3 5 9
// begin 记录每个区间的首,num 即尾部
// [begin, num)区间如果合法,则这个区间可用
// 加完后设置新的区间首为 num+1,这边的话就是6
// 注意一个情况就是,如果 [begin, num) 元素个数多了,那么只能加上应该有的个数,然后返回
// 第二,如果nums数组区间内的元素个数不够k,那么要加上从最后一个元素右边的k个元素
Arrays.sort(nums);
long sum = 0, begin = 1, cnt;
int n = nums.length;
for (int num : nums) {
if (begin < num) {
cnt = num - 1 - begin + 1 <= k ? num - begin : k;
// being + ... + num - 1
sum += cnt * (begin + begin + cnt - 1) / 2;
k -= cnt;
if (k == 0) return sum;
}
begin = num + 1;
}
sum += (long) (nums[n - 1] + 1 + nums[n - 1] + k) * k / 2;
return sum;
}
}
|
难度中等1132
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。void insert(String word) 向前缀树中插入字符串 word 。boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
class Trie {
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie root = this;
for (int i = 0; i < word.length(); i++) {
int idx = word.charAt(i) - 'a';
if (root.children[idx] == null) {
root.children[idx] = new Trie();
}
root = root.children[idx];
}
root.isEnd = true;
}
public boolean search(String word) {
Trie root = searchPrefix(word);
return root != null && root.isEnd;
}
public boolean startsWith(String prefix) {
Trie root = searchPrefix(prefix);
return root != null;
}
private Trie searchPrefix(String prefix) {
Trie root = this;
for (int i = 0; i < prefix.length(); i++) {
int idx = prefix.charAt(i) - 'a';
if (root.children[idx] == null) {
return null;
} else {
root = root.children[idx];
}
}
return root;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
|
剑指Offer
题解
找出数组中重复的数字。在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
// 如果用set或者map的话
// Time:O(n)
// Space:O(n)
// 值: 0 2 1 3 3
// 下标: 0 1 2 3 4
// 对于每个数字nums[i]如果这个数字 nums[i] 不等于其 下标 i的话,则将这个数字放到 nums[i]这个下标上,如果交换的时候发现两者相同则直接返回。
class Solution {
public int findRepeatNumber(int[] nums) {
for (int i = 0; i < nums.length; i++) {
while (nums[i] != i) {
if (nums[i] == nums[nums[i]]) {
return nums[i];
}
swap(nums, i, nums[i]);
}
}
return -1;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
// Time:O(n)
// Space:O(1)
|
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) return false;
int m = matrix.length, n = matrix[0].length;
int row = 0, col = n - 1;
while (row < m && col >= 0) {
if (matrix[row][col] == target) {
return true;
} else if (matrix[row][col] < target) {
row++;
} else {
col--;
}
}
return false;
}
}
// Time:O(m+n)
// Space:O(1)
|
难度简单211
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public String replaceSpace(String s) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == ' ') {
sb.append("%20");
} else {
sb.append(c);
}
}
return sb.toString();
}
}
// Time:O(n)
// Space:O(n)
|
难度简单234
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
// 1. 反转链表,然后正常放入值
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
public int[] reversePrint(ListNode head) {
ListNode dummy = new ListNode(0);
ListNode p = head;
int len = 0;
while (p != null) {
len++;
ListNode temp = p.next;
p.next = dummy.next;
dummy.next = p;
p = temp;
}
int[] res = new int[len];
int i = 0;
while (dummy.next != null) {
res[i++] = dummy.next.val;
dummy = dummy.next;
}
return res;
}
}
// 2. 第一个值放到最后一个位置,第二个值放到倒数第二个位置,以此类推
class Solution {
public int[] reversePrint(ListNode head) {
int len = 0;
ListNode p = head;
while (p != null) {
len++;
p = p.next;
}
int[] res = new int[len];
p = head;
for (int i = len - 1; i >= 0; i--) {
res[i] = p.val;
p = p.next;
}
return res;
}
}
// Time:O(n)
// Space:O(n)
|
难度中等663
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return helper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}
private TreeNode helper (int[] preorder, int pre_left, int pre_right, int[] inorder, int in_left, int in_right) {
if (pre_left > pre_right || in_left > in_right) return null;
TreeNode root = new TreeNode(preorder[pre_left]);
int ind = 0;
for (int i = in_left; i <= in_right; i++) {
if (inorder[i] == preorder[pre_left]) {
ind = i;
break;
}
}
int left_size = ind - 1 - in_left + 1, right_size = in_right - (ind + 1) + 1;
root.left = helper(preorder, pre_left + 1, pre_left + left_size, inorder, in_left, in_left + left_size - 1);
root.right = helper(preorder, pre_right - right_size + 1, pre_right, inorder, in_right - right_size + 1, in_right);
return root;
}
}
// Time: O(n+nlgn)->O(nlgn)
// Space:O(lgn)
|
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class CQueue {
Deque<Integer> inStack;
Deque<Integer> outStack;
public CQueue() {
inStack = new LinkedList<>();
outStack = new LinkedList<>();
}
public void appendTail(int value) {
inStack.push(value);
}
public int deleteHead() {
if (inStack.isEmpty()) {
return -1;
}
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
int head = outStack.pop();
while (!outStack.isEmpty()) {
inStack.push(outStack.pop());
}
return head;
}
}
/**
* Your CQueue object will be instantiated and called as such:
* CQueue obj = new CQueue();
* obj.appendTail(value);
* int param_2 = obj.deleteHead();
*/
|
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
1
2
|
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
|
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public int fib(int n) {
if (n == 0 || n == 1) return n;
int a = 0, b = 1;
for (int i = 2; i <= n; i++) {
int c = (a + b) % 1000000007;
a = b;
b = c;
}
return b;
}
}
|
矩阵快速幂
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
static final int MOD = 1000000007;
public int fib(int n) {
if (n < 2) {
return n;
}
int[][] q = {{1, 1}, {1, 0}};
int[][] res = pow(q, n - 1);
return res[0][0];
}
public int[][] pow(int[][] a, int n) {
int[][] ret = {{1, 0}, {0, 1}};
while (n > 0) {
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
n >>= 1; // n /= 2
a = multiply(a, a);
}
return ret;
}
public int[][] multiply(int[][] a, int[][] b) {
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
}
|
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int numWays(int n) {
if (n == 0 || n == 1) return 1;
int[] dp = new int[n + 1];
int a = 1, b = 1, c = 2;
for (int i = 2; i <= n; i++) {
c = (a + b) % 1000000007;
a = b;
b = c;
}
return c;
}
}
|
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 注意不能用mid与left进行比较进行区间缩小
class Solution {
public int minArray(int[] numbers) {
int len = numbers.length;
int left = 0, right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (numbers[mid] > numbers[right]) {
// [mid + 1, right]
left = mid + 1;
} else if (numbers[mid] < numbers[right]) {
// [left, mid]
right = mid;
} else {
// 若想等,只能将right缩小,无法确定具体区间
// 示例一 [1, 0, 1, 1, 1][1,0,1,1,1] :旋转点 x = 1x=1 ,因此 m=2,m=2 在 右排序数组 中。
// 示例二 [1, 1, 1, 0, 1][1,1,1,0,1] :旋转点 x = 3x=3 ,因此 m=2,m=2 在 左排序数组 中。
right--;
}
}
return numbers[left];
}
}
// Time:O(lgn)
// Space:O(1)
|
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
boolean flag = false;
public boolean exist(char[][] board, String word) {
if (board == null || board.length == 0) return false;
int m = board.length, n = board[0].length;
boolean[][] vis = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (dfs(board, i, j, vis, word, 0)) {
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, int i, int j, boolean[][] vis, String word, int idx) {
if (idx == word.length()) {
return true;
}
if ((i < 0 || i >= board.length) || (j < 0 || j >= board[0].length) || vis[i][j] || board[i][j] != word.charAt(idx)) {
return false;
}
vis[i][j] = true;
boolean res = dfs(board, i + 1, j, vis, word, idx + 1)
|| dfs(board, i - 1, j, vis, word, idx + 1)
|| dfs(board, i, j + 1, vis, word, idx + 1)
|| dfs(board, i, j - 1, vis, word, idx + 1);
vis[i][j] = false;
return res;
}
}
|
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int movingCount(int m, int n, int k) {
if (m == 0 || n == 0) return 0;
boolean[][] vis = new boolean[m][n];
return dfs(vis, 0, 0, k);
}
private int dfs(boolean[][] vis, int i, int j, int k) {
if ((i < 0 || i >= vis.length) || (j < 0 || j >= vis[0].length) || vis[i][j] || (i / 10 + i % 10 + j / 10 + j % 10) > k) return 0;
vis[i][j] = true;
return 1 + dfs(vis, i + 1, j, k) + dfs(vis, i, j + 1, k);
}
}
|
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int cuttingRope(int n) {
// dp[i] 表示长度为i至少剪一刀的最大乘积
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i - 1; j++) {
dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
}
}
return dp[n];
}
}
|
贪心
算法流程:
当 $n \leq 3$ 时,按照规则应不切分,但由于题目要求必须剪成 m>1 段,因此必须剪出一段长度为 1 的绳子,即返回 n - 1 。
当 $n>3n$ 时,求 n 除以 3 的 整数部分 a 和 余数部分b (即 n = 3a+b ),并分为以下三种情况:
当 b = 0 时,直接返回 $3^a$
当 b = 1 时,将$3a+1$转换为$3 \times (a-1)+3+1=3 \times (a-1)+2+2$,因此返回 $3^{a-1} \times 4$
当 b = 2 时,返回 $3^a \times 2$
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n - 1;
int res = 1;
while (n > 4) {
res = res * 3;
n -= 3;
}
res *= n;
return res;
}
}
|
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
// 1. dp
class Solution {
public int cuttingRope(int n) {
// dp[i] 表示总长度为 i 能够得到的最大乘积
// 最后一段可以长度 j 为 1 , 2, ..., i - 2
// 对于前面长度为 i - j的话可以剪,也可以不剪
// 那么结果就是 max(dp[i], max(j * dp[i - j], j * (i - j)))
// 也就是 1 * dp[i - 1], 2 * d[i - 2], ... , (i - 2) * dp[2]
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i - 2; j++) {
dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));
}
}
return dp[n];
}
}
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n - 1;
long res = 1;
while(n > 4){
res = res * 3 % 1000000007;
n -= 3;
}
return (int)(res * n % 1000000007);
}
}
|
难度简单215
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为 汉明重量).)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
// 1. 检查第i位时,将n与2^i次方进行与运算,如果与完之后等于2^i,说明该位置是1,如果与完之后等于0,说明该位置是0
// 1 0 0 1 0
// 0 0 0 1 0
public int hammingWeight(int n) {
int cnt = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) cnt++;
}
return cnt;
}
// 2. 每次检查最低位是不是1,是则计数,每次判断完最低位之后都要右移一位
public int hammingWeight_1(int n) {
int cnt = 0;
for (int i = 0; i < 32; i++) {
if ((n & 1) == 1) cnt++;
n = n >> 1;
}
return cnt;
}
// 3. 通过n & (n-1)来将n最低位的1置为0,直到n等于0为止
public int hammingWeight_2(int n) {
int cnt = 0;
while (n != 0) {
n = n & (n - 1);
cnt++;
}
return cnt;
}
}
|
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,x^n)。不得使用库函数,同时不需要考虑大数问题。
快速幂 + 递归
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public double myPow(double x, int n) {
if(n == 0) return 1;
if(n == 1) return x;
if(n == -1) return 1 / x;
// n / 2 + n / 2 + n % 2
double half = myPow(x, n / 2);
double mod = myPow(x, n % 2);
return half * half * mod;
}
}
// Time:O(lgn)
// Space:O(lgn)
|
快速幂 + 迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public double myPow(double x, int n) {
if (n == 0) return 1.0;
long b = n; // 负数最小值的绝对值超出int范围,所以用更大容量防止溢出
if (b < 0) {
x = 1 / x;
b = -b;
}
double res = 1.0;
while (b > 0) {
if ((b & 1) == 1) res *= x;
x *= x;
b /= 2;
}
return res;
}
}
// Time:O(lgn)
// Space:O(1)
|
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int[] printNumbers(int n) {
// n = 1, res = 1-9
// n = 2, res = 1-99
// n , res = 1 - 10 ^ n - 1
int len = (int) Math.pow(10, n) - 1;
int[] res = new int[len];
for (int i = 0; i < len; i++) {
res[i] = i + 1;
}
return res;
}
}
|
如果是大数,转为n位0-9的全排列问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
char[] nums = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
int[] res;
int idx;
StringBuilder path = new StringBuilder();
public int[] printNumbers(int n) {
int len = (int) Math.pow(10, n) - 1;
res = new int[len];
idx = 0;
dfs(0, n);
return res;
}
private void dfs(int cur, int n) {
if (cur == n) {
int curNum = Integer.parseInt(path.toString());
if (curNum != 0) {
res[idx++] = curNum;
}
return;
}
for (char num : nums) {
path.append(num);
dfs(cur + 1, n);
path.deleteCharAt(path.length() - 1);
}
}
}
|
难度简单192
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
// 迭代
class Solution {
public ListNode deleteNode(ListNode head, int val) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode pre = dummy;
while (pre.next.val != val) {
pre = pre.next;
}
// pre delete_node pre.next.next
pre.next = pre.next.next;
return dummy.next;
}
}
// 递归
class Solution {
public ListNode deleteNode(ListNode head, int val) {
if (head == null) return head;
if (head.val == val) {
ListNode newHead = head.next;
head.next = null;
return newHead;
}
head.next = deleteNode(head.next, val);
return head;
}
}
|
难度中等286
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。
数值(按顺序)可以分成以下几个部分:
- 若干空格
- 一个 小数 或者 整数
- (可选)一个
'e' 或 'E' ,后面跟着一个 整数
- 若干空格
小数(按顺序)可以分成以下几个部分:
- (可选)一个符号字符(
'+' 或 '-')
- 下述格式之一:
- 至少一位数字,后面跟着一个点
'.'
- 至少一位数字,后面跟着一个点
'.' ,后面再跟着至少一位数字
- 一个点
'.' ,后面跟着至少一位数字
整数(按顺序)可以分成以下几个部分:
- (可选)一个符号字符(
'+' 或 '-')
- 至少一位数字
部分数值列举如下:
["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]
部分非数值列举如下:
["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// ‘.’出现正确情况:只出现一次,且在e的前面
// ‘e’出现正确情况:只出现一次,且出现前有数字
// ‘+’‘-’出现正确情况:只能在开头和e后一位
class Solution {
public boolean isNumber(String s) {
if (s == null || s.length() == 0) return false;
//去掉首位空格
s = s.trim();
boolean numFlag = false;
boolean dotFlag = false;
boolean eFlag = false;
for (int i = 0; i < s.length(); i++) {
//判定为数字,则标记numFlag
if (s.charAt(i) >= '0' && s.charAt(i) <= '9') {
numFlag = true;
//判定为. 需要没出现过.并且没出现过e
} else if (s.charAt(i) == '.' && !dotFlag && !eFlag) {
dotFlag = true;
//判定为e,需要没出现过e,并且出过数字了
} else if ((s.charAt(i) == 'e' || s.charAt(i) == 'E') && !eFlag && numFlag) {
eFlag = true;
numFlag = false;//为了避免123e这种请求,出现e之后就标志为false
//判定为+-符号,只能出现在第一位或者紧接e后面
} else if ((s.charAt(i) == '+' || s.charAt(i) == '-') && (i == 0 || s.charAt(i - 1) == 'e' || s.charAt(i - 1) == 'E')) {
//其他情况,都是非法的
} else {
return false;
}
}
return numFlag;
}
}
|
难度简单194
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数在数组的前半部分,所有偶数在数组的后半部分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int[] exchange(int[] nums) {
int len = nums.length;
int left = 0, right = len - 1;
while (left < right) {
while ((nums[left] & 1) == 1 && left < right) left++;
while ((nums[right] & 1) == 0 && left < right) right--;
if (left < right) {
swap(nums, left, right);
}
}
return nums;
}
private void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
|
难度简单323
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode fast = new ListNode(0);
fast.next = head;
ListNode slow = fast;
while (k != 0) {
fast = fast.next;
k--;
}
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow.next;
}
}
|
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 1. 迭代,头插法
class Solution {
public ListNode reverseList(ListNode head) {
ListNode dummy = new ListNode(0);
ListNode p = head;
while (p != null) {
ListNode temp = p.next;
p.next = dummy.next;
dummy.next = p;
p = temp;
}
return dummy.next;
}
}
// 2. 递归
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) return head;
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}
|
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
ListNode pre = dummy;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
pre.next = l1;
l1 = l1.next;
} else {
pre.next = l2;
l2 = l2.next;
}
pre = pre.next;
}
if (l1 != null) {
pre.next = l1;
}
if (l2 != null) {
pre.next = l2;
}
return dummy.next;
}
}
|
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
// 1. 先序遍历树 A 中的每个节点,判断 B 是不是该子树下的子结构
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) return false;
return helper(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
// 2. 判断以 A 为根节点的子树 是否包含树 B
public boolean helper(TreeNode A, TreeNode B) {
// B 扫描完了
if (B == null) return true;
// A 扫描完了,但是 B 还没扫描完
if (A == null) return false;
if (A.val != B.val) return false;
return helper(A.left, B.left) && helper(A.right, B.right);
}
}
|
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if (root == null) return null;
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
mirrorTree(root.left);
mirrorTree(root.right);
return root;
}
}
|
难度简单283
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
return helper(root.left, root.right);
}
private boolean helper(TreeNode A, TreeNode B) {
if (A == null && B == null) return true;
if (A == null || B == null) return false;
return A.val == B.val && helper(A.left, B.right) && helper(A.right, B.left);
}
}
|
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0) return new int[0];
int m = matrix.length, n = matrix[0].length;
int len = m * n;
int[] res = new int[len];
int[][] directions = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
boolean[][] visited = new boolean[m][n];
int i = 0, j = 0, dir = 0;
// 碰到边界 或 碰到访问过的 转向
for (int ind = 0; ind < len ;ind++) {
res[ind] = matrix[i][j];
visited[i][j] = true;
int next_i = i + directions[dir][0], next_j = j + directions[dir][1];
if (next_i < 0 || next_i >= m
|| next_j < 0 ||next_j >= n
|| visited[next_i][next_j]) {
dir = (dir + 1) % 4;
}
i += directions[dir][0];
j += directions[dir][1];
}
return res;
}
}
// Time:O(MN)
// Space:O(MN) -> visited数组
// 2. ⭐⭐⭐
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0) return new int[0];
int m = matrix.length, n = matrix[0].length;
int[] res = new int[m * n];
int idx = 0;
int l = 0, r = n - 1, t = 0, b = m - 1;
while (true) {
// 上边界,从左到右
for (int j = l; j <= r; j++) res[idx++] = matrix[t][j];
if (++t > b) break;
// 右边界,从上到下
for (int i = t; i <= b; i++) res[idx++] = matrix[i][r];
if (--r < l) break;
// 下边界,从右到左
for (int j = r; j >= l; j--) res[idx++] = matrix[b][j];
if (--b < t) break;
// 左边界,从下到上
for (int i = b; i >= t; i--) res[idx++] = matrix[i][l];
if (++l > r) break;
}
return res;
}
}
// Time:O(MN)
// Space:O(1)
|
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
class MinStack {
Node dummy;
/** initialize your data structure here. */
public MinStack() {
dummy = new Node(0, 0);
}
public void push(int x) {
if (dummy.next == null) {
dummy.next = new Node(x, x);
} else {
Node node = new Node(x, Math.min(x, dummy.next.minVal));
node.next = dummy.next;
dummy.next = node;
}
}
public void pop() {
dummy.next = dummy.next.next;
}
public int top() {
return dummy.next.val;
}
public int min() {
return dummy.next.minVal;
}
private class Node {
int val;
int minVal;
Node next;
private Node(int val, int minVal) {
this(val, minVal, null);
}
private Node(int val, int minVal, Node next) {
this.val = val;
this.minVal = minVal;
this.next = next;
}
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.min();
*/
|
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Deque<Integer> stack = new LinkedList<>();
int idx = 0, len = popped.length;
for (int val : pushed) {
stack.push(val);
// // 出栈操作: 每次入栈后,循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
while (idx < len && !stack.isEmpty() && stack.peek() == popped[idx]) {
stack.pop();
idx++;
}
}
return idx == len;
}
}
|
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int[] levelOrder(TreeNode root) {
if (root == null) return new int[0];
List<Integer> res = new ArrayList<>();
Deque<TreeNode> queue = new LinkedList<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
p = queue.poll();
res.add(p.val);
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
}
int n = res.size();
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[i] = res.get(i);
}
return ans;
}
}
|
难度简单176
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList();
if (root == null) return res;
Deque<TreeNode> queue = new LinkedList<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < size; i++) {
p = queue.poll();
level.add(p.val);
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
res.add(level);
}
return res;
}
}
|
难度中等178
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList();
if (root == null) return res;
Deque<TreeNode> queue = new LinkedList<>();
int depth = 0;
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int size = queue.size();
depth++;
List<Integer> level = new ArrayList<>();
for (int i = 0; i < size; i++) {
p = queue.poll();
level.add(p.val);
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
if ((depth & 1) == 0) Collections.reverse(level);
res.add(level);
}
return res;
}
}
|
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public boolean verifyPostorder(int[] postorder) {
return helper(postorder, 0, postorder.length - 1);
}
private boolean helper(int[] postorder, int left, int right) {
if (left >= right) return true; // 结点数小于等于1肯定是对的
int i = left;
while (postorder[i] < postorder[right]) {
i++;
}
int m = i;
// [left m - 1] [m, right - 1] right
while (postorder[i] > postorder[right]) {
i++;
}
return i == right && helper(postorder, left, m - 1) && helper(postorder, m, right - 1);
}
}
|
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
if (root == null) return res;
dfs(root, target);
return res;
}
private void dfs(TreeNode root, int target) {
if (root == null) return;
path.add(root.val);
target -= root.val;
if (root.left == null && root.right == null && target == 0) {
res.add(new ArrayList<>(path));
}
dfs(root.left, target);
dfs(root.right, target);
path.remove(path.size() - 1);
target += root.val;
}
}
|
难度中等416
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
// 1. 哈希表
// Time:O(n)
// Space:O(n)
class Solution {
public Node copyRandomList(Node head) {
Node p = head;
Map<Node, Node> map = new HashMap<>();
while (p != null) {
Node node = new Node(p.val);
map.put(p, node);
p = p.next;
}
p = head;
while (p != null) {
map.get(p).next = map.get(p.next);
map.get(p).random = map.get(p.random);
p = p.next;
}
return map.get(head);
}
}
// 2. 拼接 + 拆分
// Time:O(n)
// Space:O(1)
class Solution {
public Node copyRandomList(Node head) {
if (head == null) return null;
Node p = head;
// 建立 next
while (p != null) {
Node temp = p.next;
Node p_copy = new Node(p.val);
p_copy.next = p.next;
p.next = p_copy;
p = temp;
}
// 建立 random
p = head;
while (p != null) {
if (p.random != null) p.next.random = p.random.next;
p = p.next.next;
}
Node res = head.next;
Node pre = head;
p = pre.next;
// 拆分
while (p.next != null) {
pre.next = pre.next.next;
p.next = p.next.next;
pre = pre.next;
p = p.next;
}
pre.next = null;
return res;
}
}
|
请实现两个函数,分别用来序列化和反序列化二叉树。
你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
Solution1. dfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public static final String NULL_VAL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
return root.val + " " + serialize(root.left) + " " + serialize(root.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
Deque<String> queue = new LinkedList<>(Arrays.asList(data.split(" ")));
return dfs(queue);
}
private TreeNode dfs(Deque<String> queue) {
String str = queue.poll();
if (NULL_VAL.equals(str)) return null;
TreeNode root = new TreeNode(Integer.parseInt(str));
root.left = dfs(queue);
root.right = dfs(queue);
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
|
Solution2. bfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
public static final String NULL_VAL = "#";
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return NULL_VAL;
StringBuilder sb = new StringBuilder();
Deque<TreeNode> queue = new LinkedList<>();
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
p = queue.poll();
if (p != null) {
sb.append(p.val + " ");
queue.offer(p.left);
queue.offer(p.right);
} else {
sb.append(NULL_VAL + " ");
}
}
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
Deque<String> strs = new LinkedList<>(Arrays.asList(data.split(" ")));
Deque<TreeNode> queue = new LinkedList<>();
String str = strs.poll();
if (NULL_VAL.equals(str)) return null;
TreeNode root = new TreeNode(Integer.parseInt(str));
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
String left = strs.poll();
String right = strs.poll();
if (!NULL_VAL.equals(left)) {
cur.left = new TreeNode(Integer.parseInt(left));
queue.offer(cur.left);
}
if (!NULL_VAL.equals(right)) {
cur.right = new TreeNode(Integer.parseInt(right));
queue.offer(cur.right);
}
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
|
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// dfs + 剪枝
class Solution {
List<String> res;
StringBuilder path;
boolean[] visited;
public String[] permutation(String s) {
int len = s.length();
res = new ArrayList<>();
path = new StringBuilder();
visited = new boolean[len];
char[] chars = s.toCharArray();
Arrays.sort(chars);
dfs(0, chars);
return res.toArray(new String[0]);
}
private void dfs(int cnt, char[] chars) {
if (cnt == chars.length) {
res.add(new String(path));
return;
}
for (int i = 0; i < chars.length; i++) {
if (visited[i] == true) continue;
if (i > 0 && !visited[i - 1] && chars[i] == chars[i - 1]) continue;
path.append(chars[i]);
visited[i] = true;
dfs(cnt + 1, chars);
path.deleteCharAt(path.length() - 1);
visited[i] = false;
}
}
}
|
难度简单245
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
// hashmap
class Solution {
public int majorityElement(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
int res = 0, max_cnt = 0;
for (int key : map.keySet()) {
int cnt = map.get(key);
if (cnt > max_cnt) {
res = key;
max_cnt = cnt;
}
}
return res;
}
}
// 摩尔计数法
class Solution {
public int majorityElement(int[] nums) {
// 通过计数器cnt来判断是否要还候选人
int cnt = 0;
Integer candidate = null;
for (int num : nums) {
if (cnt == 0) {
candidate = num;
cnt++;
continue;
}
if (num == candidate) {
cnt++;
} else {
cnt--;
}
}
return candidate;
}
}
|
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
- 优先队列(大根堆)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (arr == null || arr.length == 0 || k == 0) return new int[0];
PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> o2 - o1);
for (int num : arr) {
// queue.offer(num);
// if (queue.size() > k) {
// queue.poll();
// }
// **剪枝:29ms -> 17ms**
// 如果queue不满,直接插入
if (queue.size() < k) {
queue.offer(num);
} else if (num < queue.peek()) {
// 满了则要判断是否要插入重新堆化
// 如果新数字大于根结点,则跳过不用考虑,否则需要插入
queue.poll();
queue.offer(num);
}
}
int[] res = new int[queue.size()];
int i = 0;
while (!queue.isEmpty()) {
res[i++] = queue.poll();
}
return res;
}
}
|
- 快速选择
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (arr == null || arr.length == 0 || k == 0) return new int[0];
// 前k个最小元素,也就是快速选择后,找到下标为k-1的元素,[0, k-1]即所求
quickSelect(arr, 0, arr.length - 1, k - 1);
// int[] res = new int[k];
// System.arraycopy(arr, 0, res, 0, k);
// return res;
// Arrays.copyOf调用了System.arraycopy
return Arrays.copyOf(arr, k);
}
private void quickSelect(int[] arr, int left, int right, int k) {
int mid = partition(arr, left, right);
if (mid == k) {
return;
} else if (mid < k) {
quickSelect(arr, mid + 1, right ,k);
} else {
quickSelect(arr, left, mid - 1, k);
}
}
private int partition(int[] arr, int left, int right) {
int random_index = (int) (left + Math.random() * (right - left + 1));
int temp = nums[left];
nums[left] = nums[random_index];
nums[random_index] = temp;
// 加了上面的交换之后速度可能有提升,该题中不加已经超过100%
int pivot = arr[left];
while (left < right) {
while (left < right && arr[right] >= pivot) {
right--;
}
arr[left] = arr[right];
while (left < right && arr[left] <= pivot) {
left++;
}
arr[right] = arr[left];
}
arr[left] = pivot;
return left;
}
}
|
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// dp
class Solution {
public int maxSubArray(int[] nums) {
int len = nums.length;
int[] dp = new int[len];
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < len; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
res = Math.max(res, dp[i]);
}
return res;
}
}
// 空间压缩
class Solution {
public int maxSubArray(int[] nums) {
int len = nums.length;
int cur = nums[0];
int res = cur;
for (int i = 1; i < len; i++) {
cur = Math.max(nums[i], nums[i] + cur);
res = Math.max(res, cur);
}
return res;
}
}
|
难度中等371
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Solution {
public int translateNum(int num) {
if (num >= 0 && num <= 9) return 1;
String s = String.valueOf(num);
int len = s.length();
int[] dp = new int[len];
dp[0] = 1;
if (Integer.parseInt(s.substring(0, 2)) <= 25) {
dp[1] = 1 + 1;
} else {
dp[1] = 1;
}
for (int i = 2; i < len; i++) {
if (Integer.parseInt(s.substring(i - 1, i + 1)) <= 25 && s.charAt(i - 1) != '0') {
dp[i] = dp[i - 1] + dp[i - 2];
} else {
dp[i] = dp[i - 1];
}
}
return dp[len - 1];
}
}
// 空间优化
class Solution {
public int translateNum(int num) {
if (num >= 0 && num <= 9) return 1;
String s = String.valueOf(num);
int len = s.length();
int a = 1, b = 1, c = 1;
if (Integer.parseInt(s.substring(0, 2)) <= 25) {
b = 1 + 1;
} else {
b = 1;
}
for (int i = 2; i < len; i++) {
int temp = b;
if (Integer.parseInt(s.substring(i - 1, i + 1)) <= 25 && s.charAt(i - 1) != '0') {
c = a + b;
} else {
c = b;
}
b = c;
a = temp;
}
return b;
}
}
|
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public int maxValue(int[][] grid) {
if (grid == null || grid.length == 0) return 0;
int m = grid.length, n = grid[0].length;
int[][] dp = new int[m][n];
dp[0][0] = grid[0][0];
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
}
|
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
- 双指针+滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
/*
1.将字符串中的字符取出,使用HashMap存取对应字符。key对应字符,value对应字符下标。用Hashmap来判断字符串中字符是否重复
2.设Left为区间左端点下标,right为区间右端点下标。即区间长度=right-left+1;
3.区间左端点left不动,让right这个右端点往后遍历,如果发现准备放入map的字符已经在Hashmap中存在,那么只需要将左端点更新到在map已经存在的字符的右边一个位置,即已存在字符的下标+1。 比如aba,左端点下标开始是0,第二个a准备存入map时,发现map中已经存在a了,所以将区间左端点下标更新为第一个a的右边位置,即第一个a的下标+1。子串ab,因此变成子串 ba。
至于为什么左端点要更新到已存在字符的右边一个位置,因为关键字是最长子串。如 aba,遍历字符串aba,准备放入第二个a时发现map已经存在了字符a,那么为了保证题意的最长子串。由于子串ab,和子串ba的长度显然都是2,二者虽然长度一样。但ab子串不可能再变长(ab子串右边有一个a了,限制了子串的成长)。而ba子串向后面遍历字符串还有可能接像c,d等其他字符,子串长度成长空间更大,显然符合求最长子串的题意。要选出更长的子串,Left必须更新。
4.注意:left = Math.max(left,map.get(s.charAt(i))+1); 之所以这里要取最大值,而不是直接让left = map.get(s.charAt(i))+1
是因为 存在 abba这种回文情况,如果left = map.get(s.charAt(i))+1 ,当第二个b存入map时,Left更新为2。当第二个a,准备存入map时,如果不取最大值,会导致本来是left本来是2,又更新变成为1,出现了left往回退的情况。而left = Math.max(left,map.get(s.charAt(i))+1)可以避免这个情况。
另外由于是HashMap的原因, map.get(s.charAt(i))的值如果存在,肯定是前一次相同字符存储好的下标。 所以每次对新的字符判断map是否存在后, 无论是否更新left,也都要在map中更新每次新字符对应的新下标。 比如abba,首先子串为ab,后面子串更新为ba后,b的下标更新为2而不是1,a的下标更新为3,而不是1.如果不更新新字符对应下标 比如abbabc这种情况,后面遍历到第三个b时,本来left要更新到第二个b的后面也就第二个a的位置,但因为没在map中将第二个b的位置替换为第一个b的位置,而导致出错。
作者:unique_cat
链接:https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/solution/javasi-lu-xiang-jie-xiao-bai-jiu-xing-by-wfbf/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
*/
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map = new HashMap<>();
int ans = 0;
for (int left = 0, right = 0; right < s.length(); right++) {
if (map.containsKey(s.charAt(right))) {
left = Math.max(left, map.get(s.charAt(right)) + 1);
}
ans = Math.max(ans, right - left + 1);
map.put(s.charAt(right), right);
}
return ans;
}
}
// 优化:用数组代替map,map的作用就是记录当前这个窗口中什么时候出现了这个新的重复的元素,那么每次记录下每个元素的下标就可以了
class Solution {
public int lengthOfLongestSubstring(String s) {
int[] last = new int[128];
for (int i = 0; i < 128; i++) {
last[i] = -1;
}
int ans = 0;
for (int left = 0, right = 0; right < s.length(); right++) {
if (last[s.charAt(right)] != -1) {
left = Math.max(left, last[s.charAt(right)] + 1);
}
ans = Math.max(ans, right - left + 1);
last[s.charAt(right)] = right;
}
return ans;
}
}
|
- 动态规划
1
2
3
4
5
6
|
dp[j]表示以下标为j字符结尾的不含重复字符的子字符串
设dp[i] == dp[j],i < j
1.i < 0, 说明j左边没有元素和当前元素相同,dp[j] = dp[j - 1] + 1
2. i > 0
2.1 dp[j - 1]>len((i, j]) = j - i,说明s[i]在以j-1为结尾的结果里面,dp[j] = j - i
2.2 dp[j - 1]<=len((i, j]) = j - i,说明s[i]在以j-1为结尾的结果外面,dp[j] = dp[j - 1] + 1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
class Solution {
public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) return 0;
int n = s.length();
int[] dp = new int[n];
Map<Character, Integer> map = new HashMap<>();
dp[0] = 1;
map.put(s.charAt(0), 0);
int res = 1;
for (int i = 1; i < n; i++) {
if (!map.containsKey(s.charAt(i))) {
dp[i] = Math.max(dp[i], 1 + dp[i - 1]);
} else {
if (map.get(s.charAt(i)) < i - dp[i - 1]) {
dp[i] = Math.max(dp[i], 1 + dp[i - 1]);
} else {
dp[i] = Math.max(dp[i], i - map.get(s.charAt(i)));
}
}
res = Math.max(res, dp[i]);
map.put(s.charAt(i), i);
}
return res;
}
}
// 优化1:每次dp[i]只依赖于dp[i-1],所以可以不用数组,用两个变量
// 优化2:对于map只是用来记录上一次元素出现的位置,可以不用map用数组
class Solution {
public int lengthOfLongestSubstring(String s) {
int res = 0, last = 0, len = s.length();
Map<Character, Integer> map = new HashMap<>();
for (int i = 0; i < len; i++) {
char c = s.charAt(i);
last = Math.min(i - map.getOrDefault(c, -1), last + 1);
res = Math.max(res, last);
map.put(c, i);
}
return res;
}
}
|
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
// 三指针
// 第一个丑数是1,以后的丑数都是基于前面的小丑数分别乘2,3,5构成的。
// 我们每次添加进去一个当前计算出来个三个丑数的最小的一个,并且是谁计算的,谁指针就后移一位。
class Solution {
public int nthUglyNumber(int n) {
int a = 0, b = 0, c = 0;
int[] res = new int[n];
res[0] = 1;
for (int i = 1; i < n; i++) {
int val2 = res[a] * 2, val3 = res[b] * 3, val5 = res[c] * 5;
int minVal = Math.min(Math.min(val2, val3), val5);
res[i] = minVal;
if (minVal == val2) a++;
if (minVal == val3) b++;
if (minVal == val5) c++;
}
return res[n - 1];
}
}
|
在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
// hashmap存储个数,两次遍历字符串
// Time:O(n)
// Space:O(n)
class Solution {
public char firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>();
for (char c : s.toCharArray()) {
map.put(c, map.getOrDefault(c, 0) + 1);
}
for (char c : s.toCharArray()) {
if (map.get(c) == 1) {
return c;
}
}
return ' ';
}
}
// 执行用时:25 ms, 在所有 Java 提交中击败了35.82% 的用户
// 内存消耗:41.6 MB, 在所有 Java 提交中击败了15.97% 的用户
// 不用计数,只判断是否只出现1次
class Solution {
public char firstUniqChar(String s) {
Map<Character, Boolean> map = new HashMap<>();
for (char c : s.toCharArray()) {
// 只有0->1时才返回true
// 其他情况都是false
map.put(c, !map.containsKey(c));
}
for (char c : s.toCharArray()) {
if (map.get(c)) {
return c;
}
}
return ' ';
}
}
// 执行用时: 21 ms , 在所有 Java 提交中击败了 50.96% 的用户
// 内存消耗: 41.5 MB , 在所有 Java 提交中击败了 18.06% 的用户
|
输入两个链表,找出它们的第一个公共节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
// 常规思路,让长的链表先走多出来的部分,然后一起走
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) return null;
int lenA = 0, lenB = 0;
ListNode pA = headA, pB = headB;
while (pA != null) {
lenA++;
pA = pA.next;
}
while (pB != null) {
lenB++;
pB = pB.next;
}
int minus = Math.abs(lenA - lenB);
if (lenA < lenB) {
pA = headB;
pB = headA;
} else {
pA = headA;
pB = headB;
}
// pA指向较长的链 长度多 minus
for (int i = 0; i < minus; i++) {
pA = pA.next;
}
while (pA != pB) {
pA = pA.next;
pB = pB.next;
}
return pA;
}
}
// 非常规思路,走完自己的再走对方的
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode pA = headA, pB = headB;
while (pA != pB) {
pA = pA != null ? pA.next : headB;
pB = pB != null ? pB.next : headA;
}
return pA;
}
}
// 还可以先记录一个链表的结点,然后遍历另一个链表,判断是否结点是否存在
|
统计一个数字在排序数组中出现的次数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
// 1. 遍历 O(n) O(1)
class Solution {
public int search(int[] nums, int target) {
int cnt = 0;
for (int num : nums) {
if (num == target) {
cnt++;
}
}
return cnt;
}
}
// 2. 二分法,找第一个target,找最后一个target O(lgn) O(1)
class Solution {
public int search(int[] nums, int target) {
if (nums == null || nums.length == 0) return 0;
int first = findFirst(nums, target);
if (first == -1) return 0;
int last = findLast(nums, target);
return last - first + 1;
}
private int findFirst(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left] == target ? left : -1;
}
private int findLast(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid;
}
}
return nums[left] == target ? left : -1;
}
}
|
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
// 1. 暴力法
class Solution {
public int missingNumber(int[] nums) {
int len = nums.length;
// [0, len]
for (int i = 0; i < len; i++) {
if (nums[i] != i) {
return i;
}
}
return len;
}
}
// 2. 二分法
// 如果当前位置,下标和数字不同,说明在之前某个位置(包含当前位置)发生了错位
class Solution {
public int missingNumber(int[] nums) {
int len = nums.length;
int left = 0, right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] != mid) {
right = mid;
} else {
left = mid + 1;
}
}
// left最后的位置依然不错位,说明在数组外发生了错位,及len处
if (nums[left] == left) {
return len;
} else {
return left;
}
}
}
|
给定一棵二叉搜索树,请找出其中第 k 大的节点的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int kthLargest(TreeNode root, int k) {
int cnt = 0;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode p = root;
while (!stack.isEmpty() || p != null) {
if (p != null) {
stack.push(p);
p = p.right;
} else {
p = stack.pop();
if (++cnt == k) {
return p.val;
}
p = p.left;
}
}
return -1;
}
}
|
难度简单164
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
// 递归
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
}
// 迭代,层序遍历
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
Deque<TreeNode> queue = new LinkedList<>();
int depth = 0;
TreeNode p = root;
queue.offer(p);
while (!queue.isEmpty()) {
int size = queue.size();
depth++;
for (int i = 0; i < size; i++) {
p = queue.poll();
if (p.left != null) queue.offer(p.left);
if (p.right != null) queue.offer(p.right);
}
}
return depth;
}
}
|
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
// 自顶向下递归
// O(nlgn) O(n)
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
int leftDepth = getDepth(root.left), rightDepth = getDepth(root.right);
return Math.abs(leftDepth - rightDepth) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
private int getDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(getDepth(root.left), getDepth(root.right));
}
}
// 自底向上递归
// O(n) O(n)
// 对于某个结点,判断以其为根的树是否平衡,平衡返回高度,否则返回-1
class Solution {
public boolean isBalanced(TreeNode root) {
return getDepth(root) >= 0;
}
private int getDepth(TreeNode root) {
if (root == null) return 0;
int leftDepth = getDepth(root.left), rightDepth = getDepth(root.right);
if (leftDepth == -1 || rightDepth == -1 || Math.abs(leftDepth - rightDepth) > 1) {
return -1;
} else {
return Math.max(leftDepth, rightDepth) + 1;
}
}
}
|
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public int[] singleNumbers(int[] nums) {
int x = 0;
for (int num : nums) {
x ^= num;
}
// x = a ^ b
// 由于 a 和 b不同所以x不为0,假设x为 0100 0010
// 那么1的位置表明a和b这两个该位上不同,即该位一个为0一个为1
// 因此可以根据该为0还是1分为两组
// 每组里面都有若干相等的数加上a/b
int idx = 0;
while ((num & 1) == 0) {
num >>= 1;
idx++;
}
int a = 0, b = 0;
for (int num : nums) {
if ((num >> idx) & 1 == 0) {
a ^= num;
} else {
b ^= num;
}
}
return new int[]{a, b};
}
}
|
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int singleNumber(int[] nums) {
// 将所有数字二进制位对应加起来
// 如果该位为3,说明结果该位为0,否则结果该位为1
int len = nums.length;
int[] bit_sum = new int[32];
for (int num : nums) {
for (int j = 0; j < 32; j++) {
// num & 1 = 1说明num最低位为1,即num & 1表示最低位数字
bit_sum[j] += (num & 1);
num >>= 1;
}
}
int res = 0;
for (int i = 31; i >= 0; i--) {
res <<= 1;
if (bit_sum[i] % 3 == 1) {
res = (res | 1);
}
}
return res;
}
}
|
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
// 1. 暴力法 O(n^2) O(1)
// 2. map存num对应的下标,每次遍历到新数字看看能否找到对应剩余数字,将新数字加入到map中 O(n) O(n)
// 考虑到数字有序,可以进一步优化
// 3. 二分 暴力法的优化 O(nlgn) O(1)
// 4. 双指针
// 1. 暴力法 超时
// 2. map空间换时间
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
int[] res= new int[2];
for (int i = 0; i < nums.length; i++) {
if (map.containsKey(target - nums[i])) {
res[0] = nums[i];
res[1] = target - nums[i];
}
map.put(nums[i], i);
}
return res;
}
}
// 3. 二分法
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
for (int i = 0; i < nums.length - 1; i++) {
int find = target - nums[i];
int left = i + 1, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < find) {
left = mid + 1;
} else {
right = mid;
}
}
if (nums[left] == find) {
return new int[]{nums[i], find};
}
}
return res;
}
}
// 4. 双指针
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
int left = 0, right = nums.length - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
return new int[]{nums[left], nums[right]};
} else if (sum > target) {
right--;
} else {
left++;
}
}
return res;
}
}
|
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
// 双指针1
class Solution {
public int[][] findContinuousSequence(int target) {
// [a, b] 由于连续,所以这个范围的求和可以直接用求和公式
// sum = (b - a + 1) (a + b) / 2,注意double和int转换
List<int[]> res = new ArrayList<>();
int left = 1, right = 1;
// while (right < target) {
// 此处的判断条件可以优化,不一定要遍历完
// 当 right == target / 2 + 1的时候就是最后可能的右边界
while (right <= target / 2 + 1) {
int sum = (right - left + 1) * (right + left) / 2;
if (sum == target) {
int[] temp = new int[right - left + 1];
for (int i = 0; i < right - left + 1; i++) {
temp[i] = i + left;
}
res.add(temp);
left++;
} else if (sum < target) {
right++;
} else {
left++;
}
}
return res.toArray(new int[0][]);
}
}
// 双指针2
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> list = new ArrayList<>();
//区间是(1, 2, 3, ..., target - 1)
//套滑动窗口模板,l是窗口左边界,r是窗口右边界,窗口中的值[l, r]一定是连续值。
//当窗口中数字和小于target时,r右移; 大于target时,l右移; 等于target时就获得了一个解
for (int l = 1, r = 1, sum = 0; r <= target / 2 + 1; r++) {
sum += r;
while (sum > target) {
sum -= l++;
}
if (sum == target) {
int[] temp = new int[r - l + 1];
for (int i = 0; i < temp.length; i++) {
temp[i] = l + i;
}
list.add(temp);
}
}
return list.toArray(new int[0][]);
}
}
|
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串"I am a student. “,则输出"student. a am I”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 用split划分
class Solution {
public String reverseWords(String s) {
s = s.trim();
String[] splits = s.split(" +");
StringBuilder sb = new StringBuilder();
for (int i = splits.length - 1; i >= 0; i--) {
sb.append(splits[i]);
if (i != 0) sb.append(" ");
}
return sb.toString();
}
}
// 双指针,从后往前寻找单词,j指向单词结尾,i指向单词开头。遍历完空格之后重新设置j为空格前一个字符
class Solution {
public String reverseWords(String s) {
s = s.trim();
int len = s.length();
int j = len - 1, i = j;
StringBuilder sb = new StringBuilder();
while (i >= 0) {
while (i >= 0 && s.charAt(i) != ' ') i--;
// [i + 1, j + 1)
sb.append(s.substring(i + 1, j + 1));
sb.append(" ");
while (i >= 0 && s.charAt(i) == ' ') i--;
j = i;
}
return sb.toString().trim();
}
}
|
难度简单193
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串"abcdefg"和数字2,该函数将返回左旋转两位得到的结果"cdefgab"。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
// O(n) O(n)
class Solution {
public String reverseLeftWords(String s, int n) {
StringBuilder sb = new StringBuilder();
// [0, n) [n:)
sb.append(s.substring(n));
sb.append(s.substring(0, n));
return sb.toString();
}
}
// O(n) O(1)
// abc defg
// cba gfed 分别逆序
// defg abc 整体逆序
class Solution {
public String reverseLeftWords(String s, int n) {
int len = s.length();
StringBuilder sb = new StringBuilder(s);
reverse(sb, 0, n- 1);
reverse(sb, n, len - 1);
reverse(sb, 0, len - 1);
return sb.toString();
}
private void reverse(StringBuilder sb, int left, int right) {
while (left < right) {
char temp = sb.charAt(left);
sb.setCharAt(left, sb.charAt(right));
sb.setCharAt(right, temp);
left++;
right--;
}
}
}
|
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class MaxQueue {
Deque<Integer> queue; // 正常queue进行增减元素
Deque<Integer> desc_stack; // 单调递减栈,当前队列中的元素递减排列
public MaxQueue() {
queue = new LinkedList<>();
desc_stack = new LinkedList<>();
}
public int max_value() {
return desc_stack.isEmpty() ? -1 : desc_stack.peekFirst();
}
public void push_back(int value) {
queue.offerLast(value);
while (!desc_stack.isEmpty() && value > desc_stack.peekLast()) {
desc_stack.pollLast();
}
desc_stack.offerLast(value);
}
public int pop_front() {
if (queue.isEmpty()) return -1;
// int frontVal = queue.pollFirst();
// if (frontVal == desc_stack.peekFirst()) {
// desc_stack.pollFirst();
// }
// return frontVal;
//最好用equals来进行Integer值的判断
if (queue.peekFirst().equals(desc_stack.peekFirst())) {
desc_stack.pollFirst();
}
return queue.pollFirst();
}
}
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue obj = new MaxQueue();
* int param_1 = obj.max_value();
* obj.push_back(value);
* int param_3 = obj.pop_front();
*/
|
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public double[] dicesProbability(int n) {
double[] res = new double[6 * n - n + 1];
double all = Math.pow(6, n);
int[][] dp = new int[n + 1][6 * n + 1];
// dp[n][s] 表示 n 个骰子总和为 s 的排列数
// dp[n][s] <- dp[n-1][s-1] + dp[n-1][s-2] + dp[n-1][s-6]
for (int j = 1; j <= 6; j++) {
dp[1][j] = 1;
}
for (int i = 1; i <= n; i++) { // i个骰子
for (int j = i; j <= 6 * i; j++) { // i个骰子能够得到的总和为j
for (int k = 1; k <= 6; k++) { // 当前骰子的值为k
dp[i][j] += j - k > 0 ? dp[i - 1][j - k] : 0;
}
if (i == n) {
res[j - i] = dp[i][j] / all;
}
}
}
return res;
}
}
|
从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public boolean isStraight(int[] nums) {
// 除了0以外,剩下的 最大值 - 最小值 < 5且无重复
Set<Integer> set = new HashSet<>();
int maxVal = -1, minVal = 14;
for (int num : nums) {
if (num == 0) continue;
if (set.contains(num)) return false;
set.add(num);
maxVal = Math.max(maxVal, num);
minVal = Math.min(minVal, num);
}
return maxVal - minVal < 5;
}
}
|
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// 1. 模拟
class Solution {
public int lastRemaining(int n, int m) {
List<Integer> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
list.add(i);
}
int idx = 0;
while (n > 1) {
idx = (idx + m - 1) % n;
list.remove(idx);
n--;
}
return list.get(0);
}
}
// 2. 公式:(当前index + m) % 上一轮剩余数字的个数
class Solution {
public int lastRemaining(int n, int m) {
// (当前idx + m)% 上一轮剩余个数 = 上一轮idx
int idx = 0;
for (int len = 2; len <= n; len++) {
idx = (idx + m) % len;
}
return idx;
}
}
|
难度中等213
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public int maxProfit(int[] prices) {
// dp[i][0] 表示第i天不持股的当前利润
// dp[i][1] 表示第i天持股的当前利润
if (prices == null || prices.length == 0) return 0;
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
}
return dp[n - 1][0];
}
}
// 空间优化
class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int n = prices.length;
int no_keep = 0, keep = -prices[0];
for (int i = 1; i < n; i++) {
no_keep = Math.max(no_keep, keep + prices[i]);
keep = Math.max(keep, -prices[i]);
}
return no_keep;
}
}
|
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// 1. 数学法 用到了运算符
// 2. 迭代 用到了循环判断
// 3. 递归 用到了if边界判断
class Solution {
public int sumNums(int n) {
if (n == 1) return 1;
n += sumNums(n - 1);
return n;
}
}
// 那么就思考如何才能在 n==1的时候结束递归,不执行下面递归语句
// 短路效应
// if(A && B) // 若 A 为 false ,则 B 的判断不会执行(即短路),直接判定 A && B 为 false
// if(A || B) // 若 A 为 true ,则 B 的判断不会执行(即短路),直接判定 A || B 为 true
// 我们需要在n==1的时候不执行n += sumNums(n - 1);
class Solution {
public int sumNums(int n) {
boolean flag = (n > 1) && (n += sumNums(n - 1)) > 0;
return n;
}
}
class Solution {
public int sumNums(int n) {
boolean flag = (n == 1) || (n += sumNums(n - 1)) > 0;
return n;
}
}
|
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public int add(int a, int b) {
// ^ 亦或相当于 无进位的求和
// & 与 相当于求每位的进位数
// (a^b) ^ ((a&b)<<1)
while (b != 0) {
int c = (a & b) << 1; // 新的进位
a ^= b;
b = c;
}
return a;
}
}
|
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public int[] constructArr(int[] a) {
if (a == null || a.length == 0) return new int[0];
// 对于 b[i] 值为 a[0] * ... * a[i - 1] 1 a[i + 1] * .. * a[n - 1]
int n = a.length;
int[] b = new int[n];
// prefix[i] 表示 [0, i - 1]的乘积
// suffix[i] 表示 [i + 1, n - 1]的乘积
int[] prefix = new int[n], suffix = new int[n];
prefix[0] = 1;
for (int i = 1; i < n; i++) {
prefix[i] = prefix[i - 1] * a[i - 1];
}
suffix[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
suffix[i] = suffix[i + 1] * a[i + 1];
}
for (int i = 0; i < n; i++) {
b[i] = prefix[i] * suffix[i];
}
return b;
}
}
|
难度简单204
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return null;
if (root.val > Math.max(p.val, q.val)) {
return lowestCommonAncestor(root.left, p, q);
}
if (root.val < Math.min(p.val, q.val)) {
return lowestCommonAncestor(root.right, p, q);
}
return root;
}
}
|
难度简单376
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return null;
if (root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) return root;
if (left != null) return left;
if (right != null) return right;
return null;
}
}
|

